Trouver la dérivée : algorithme et exemples de solutions. Dérivée d'une somme algébrique de fonctions

Questions pour l'examen dans la discipline académique « Éléments de mathématiques supérieures »

pour la spécialité 230115 « Programmation dans les systèmes informatiques »

Année académique 2012\2013.

Matrices et opérations sur celles-ci.

(À PROPOS DE. Une matrice nulle est une matrice dont les éléments sont tous égaux à 0.

À PROPOS DE. Deux matrices de même dimension mxn sont appelées égal, si à l'intersection de la i-ème ligne et de la j-ème colonne dans l'une et l'autre matrice il y a le même nombre ; je=1, 2, ..., m ; j=1, 2, ..., n .

Laisser UN= (a ij) est une matrice et g est un nombre arbitraire, alors g UN= (g a ij), c'est-à-dire que lorsque la matrice A est multipliée par le nombre g, tous les nombres qui composent la matrice A sont multipliés par le nombre g.

Soient A et B des matrices de même dimension A = (a ij), B = (b ij), alors leur somme A + B est la matrice C = (c ij) de même dimension, déterminée à partir de la formule c ij = a ij + b ij, c'est-à-dire que lors de l'ajout de deux matrices, les nombres qui s'y trouvent de manière identique sont ajoutés par paires.

La matrice A peut être multipliée par la matrice B, c'est-à-dire que la matrice C = AB peut être trouvée si le nombre de colonnes n de la matrice A est égal au nombre de lignes de la matrice B, et la matrice C aura autant de lignes que la matrice A. comporte des lignes et autant de colonnes que la matrice comporte de colonnes B. Chaque élément de la matrice C est défini par une formule.

L'élément c ij de la matrice produit C est égal à la somme des produits des éléments de la i -ligne de la première matrice factorielle par les éléments correspondants de la j -ième colonne de la deuxième matrice factorielle.

Le concept de déterminant et ses propriétés.

Ce terme a d'autres significations, voir Déterminant (valeurs) .

Déterminant(ou déterminant) - l'un des concepts de base algèbre linéaire. Déterminant matrices est polynômeà partir des éléments d'une matrice carrée (c'est-à-dire une matrice dans laquelle le nombre de lignes et de colonnes est égal). En général matrice peut être défini sur n’importe quel commutatif anneau, dans ce cas le déterminant sera un élément du même anneau.

PROPRIÉTÉ 1. La valeur du déterminant ne changera pas si toutes ses lignes sont remplacées par des colonnes, et chaque ligne est remplacée par une colonne avec le même numéro, c'est-à-dire

PROPRIÉTÉ 2. Réorganiser deux colonnes ou deux lignes d'un déterminant équivaut à le multiplier par -1.

PROPRIÉTÉ 3. Si le déterminant a deux colonnes identiques ou deux lignes identiques, alors il est égal à zéro.

PROPRIÉTÉ 4. Multiplier tous les éléments d'une colonne ou d'une ligne d'un déterminant par n'importe quel nombre k équivaut à multiplier le déterminant par ce nombre k.

PROPRIÉTÉ 5. Si tous les éléments d'une colonne ou d'une ligne sont égaux à zéro, alors le déterminant lui-même est égal à zéro. Cette propriété est un cas particulier de la précédente (pour k=0).

PROPRIÉTÉ 6. Si les éléments correspondants de deux colonnes ou de deux lignes d'un déterminant sont proportionnels, alors le déterminant est égal à zéro.

PROPRIÉTÉ 7. Si chaque élément de la n-ième colonne ou de la n-ième ligne du déterminant est la somme de deux termes, alors le déterminant peut être représenté comme la somme de deux déterminants, dont un dans la n-ième colonne ou , respectivement, dans la n-ème rangée se trouve le premier des termes mentionnés et l'autre - le second ; les éléments se trouvant aux places restantes sont les mêmes pour les jalons des trois déterminants.

PROPRIÉTÉ 8. Si aux éléments d'une certaine colonne (ou d'une ligne) nous ajoutons les éléments correspondants d'une autre colonne (ou d'une autre ligne), multipliés par un facteur commun, alors la valeur du déterminant ne changera pas. Par exemple. D'autres propriétés des déterminants sont liées aux concepts de complément algébrique et de mineur. Le mineur d'un élément est un déterminant obtenu à partir d'un élément donné en barrant la ligne et la colonne à l'intersection desquelles se trouve cet élément.

Le complément algébrique de tout élément du déterminant est égal au mineur de cet élément, pris avec son signe si la somme des nombres de la ligne et de la colonne à l'intersection desquelles se trouve l'élément est un nombre pair, et avec le signe opposé si ce nombre est impair.

On désignera le complément algébrique d'un élément par une lettre majuscule du même nom et du même chiffre que la lettre qui désigne l'élément lui-même.

PROPRIÉTÉ 9. Le déterminant est égal à la somme des produits des éléments de n'importe quelle colonne (ou ligne) par leurs compléments algébriques. En d’autres termes, les égalités suivantes sont vérifiées :

Calcul des déterminants.

Le calcul des déterminants est basé sur leurs propriétés connues, qui s'appliquent aux déterminants de tous ordres. Voici les propriétés :

1. Si vous réorganisez deux lignes (ou deux colonnes) du déterminant, le déterminant changera de signe.

2. Si les éléments correspondants de deux colonnes (ou deux lignes) du déterminant sont égaux ou proportionnels, alors le déterminant est égal à zéro.

3. La valeur du déterminant ne changera pas si vous échangez les lignes et les colonnes, en conservant leur ordre.

4. Si tous les éléments d'une ligne (ou d'une colonne) ont un facteur commun, alors celui-ci peut être retiré du signe déterminant.

5. La valeur du déterminant ne changera pas si les éléments correspondants d'une autre ligne (ou colonne) sont ajoutés aux éléments d'une ligne (ou colonne), multipliés par le même nombre. Pour les déterminants du troisième ordre, cette propriété peut s’écrire par exemple ainsi :

6. Le déterminant du second ordre est calculé à l'aide de la formule

7. Le déterminant du troisième ordre est calculé à l'aide de la formule

Il existe un schéma pratique pour calculer le déterminant du troisième ordre (voir Fig. 1 et Fig. 2).

D'après le schéma présenté à la Fig. 1, les produits des éléments connectés sont pris avec leur propre signe, et selon le schéma de la Fig. 2 - avec revers. La valeur du déterminant est égale à la somme algébrique des six produits résultants.

Systèmes d'équations linéaires. Concepts et définitions de base.

Systèmemр équations algébriques linéaires Avecn inconnu(ou, système linéaire, également utilisé abréviation SLAU)V algèbre linéaire est un système d'équations de la forme

Un système d'équations linéaires à trois variables détermine l'ensemble avions. Le point d'intersection est la solution.

Voici le nombre d'équations, et c'est le nombre d'inconnues. x 1 , x 2 , …, x n- des inconnues à déterminer. un 11 , un 12 , …, un minute- les coefficients du système - et b 1 , b 2 , … b m- les membres libres - sont supposés connus . Indices de coefficients ( un je) les systèmes désignent les numéros d'équation ( je) et inconnu ( j), auquel se situe ce coefficient, respectivement .

Le système (1) est appelé homogène , si tous ses termes libres sont égaux à zéro ( b 1 = b 2 = … = b m= 0), sinon - hétérogène.

Le système (1) est appelé carré , si numéro méquations égales au nombre n inconnu.

Solution systèmes (1) - ensemble n Nombres c 1 , c 2 , …, c n, de telle sorte que la substitution de chacun c je au lieu de x je dans le système (1) transforme toutes ses équations en identités.

Le système (1) est appelé articulation , s'il a au moins une solution, et non conjoint, si elle n'a pas de solution unique.

Un système commun de type (1) peut avoir une ou plusieurs solutions.

Solutions c 1 (1) , c 2 (1) , …, c n(1) et c 1 (2) , c 2 (2) , …, c n(2) les systèmes communs de la forme (1) sont appelés divers, si au moins une des égalités est violée :

c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , …, c n (1) = c n (2) .

Un système commun de la forme (1) est appelé certain , s'il a une solution unique ; s'il a au moins deux solutions différentes, alors on l'appelle incertain. S’il y a plus d’équations que d’inconnues, cela s’appelle redéfini .

Méthodes de résolution de systèmes d'équations linéaires (méthode Cramer et Gauss).

Méthode Gauss - méthode de solution classique systèmes d'équations algébriques linéaires(SLAU). C'est la méthode d'élimination séquentielle variables, lorsque, à l'aide de transformations élémentaires, un système d'équations est réduit à un système triangulaire équivalent, à partir duquel toutes les autres variables sont trouvées séquentiellement, en commençant par la dernière variable (en nombre) .

Méthode de Cramer (règle de Cramer)- méthode de résolution des carrés systèmes d'équations algébriques linéaires avec non nul déterminant matrice principale(et pour de telles équations, il existe une solution unique). Appelé par son nom Gabriel Kramer(1704-1752), qui a inventé la méthode.

Vecteurs. Opérations linéaires sur eux.

Un vecteur est un segment orienté. Si le début d’un vecteur est au point A et la fin au point B, alors le vecteur est désigné AB. Si le début et la fin du vecteur ne sont pas indiqués, alors il est désigné par une lettre minuscule de l'alphabet latin a, b, c,…. BA désigne un vecteur dirigé à l'opposé du vecteur AB. Un vecteur dont le début et la fin coïncident est appelé zéro et noté ō. Sa direction est incertaine.

La longueur ou module d'un vecteur est la distance entre son début et sa fin. Enregistrements |AB| et |une| désignent les modules des vecteurs AB et a.

Les vecteurs sont dits colinéaires s’ils sont parallèles à une même droite, et coplanaires s’ils sont parallèles au même plan.

Deux vecteurs sont dits égaux s’ils sont colinéaires, ont la même direction et sont de même longueur.

Les opérations linéaires sur les vecteurs comprennent :

1) multiplication d'un vecteur par un nombre (Le produit d'un vecteur a et d'un nombre α est un vecteur noté α∙a. (ou vice versa a∙α), dont le module est égal à |α a| =| α||a|, et la direction coïncide avec la direction du vecteur a, si α>0, et l'inverse si α< 0.

2) addition de vecteurs (La somme des vecteurs est un vecteur, noté , dont le début est au début du premier vecteur a 1, et la fin est à la fin du dernier vecteur a n, une ligne brisée composée d'une suite de termes de vecteurs. Cette règle d'addition est appelée règle de fermeture de la ligne brisée dans le cas où la somme de deux vecteurs est équivalente à la règle du parallélogramme.

La droite e sur laquelle est donnée une direction, considérée comme positive, est appelée axe e.

Une combinaison linéaire de vecteurs a i est un vecteur a, défini par la formule , où sont des nombres.

Si pour un système de n vecteurs a i l'égalité

n’est vrai que si ce système est dit linéairement indépendant. Si l'égalité (1) est satisfaite pour , dont au moins un est différent de zéro, alors le système de vecteurs ai est dit linéairement dépendant. Par exemple, tous les vecteurs colinéaires, trois vecteurs coplanaires, quatre vecteurs ou plus dans un espace tridimensionnel sont toujours linéairement dépendants.

Trois vecteurs ordonnés linéairement indépendants ē 1, ē 2, ē 3 dans l'espace sont appelés base. Un triplet ordonné de vecteurs non coplanaires forme toujours une base. Tout vecteur a dans l'espace peut être développé selon la base ē 1, ē 2, ē 3, c'est-à-dire représenter a comme une combinaison linéaire de vecteurs de base : a= xē 1 + yē 2 + zē 3, où x, y, z sont les vecteurs de coordonnées a dans la base ē 1, ē 2, ē 3. Une base est dite orthonormée si ses vecteurs sont perpendiculaires entre eux et ont une longueur unitaire. Une telle base est notée i, j, k, c'est-à-dire i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1).

Exemple 5. Les vecteurs sont spécifiés dans une base orthonormée i, j, k par les coordonnées : a=(2;-1;8), e 1 = (1,2,3), e 2 = (1,-1,- 2), e 3 = (1,-6,0). Assurez-vous que le triplet e 1, e 2, e 3 forme une base, et trouvez les coordonnées du vecteur dans cette base.

Solution. Si le déterminant , composé des coordonnées des vecteurs e 1, e 2, e 3, n'est pas égal à 0, alors les vecteurs e 1, e 2, e 3 sont linéairement indépendants et forment donc une base. On s'assure que = -18-4+3-12=-31 Ainsi, le triple e 1, e 2, e 3 est la base.

Notons les coordonnées du vecteur a dans la base e 1 , e 2 , e 3 par x, y, z. Alors a = (x,y,z) = xe 1 + yе 2 + ze 3. Puisque par condition a = 2i – j +8k, e 1 = i +2j +3k, e 2 = i – j -2k, e 3 = i – 6j, alors à partir de l'égalité a = xe1 + ye 2 + ze 3 it s'ensuit que 2i – j +8k = xi + 2xj + 3xk + yi – yj -2yk +zi -6zj = (x+y+z)i +(2x-y-6z)j +(3x-2y)k. . Comme vous pouvez le voir, le vecteur du côté gauche de l'égalité résultante est égal au vecteur du côté droit, et cela n'est possible que si leurs coordonnées correspondantes sont égales. De là, nous obtenons un système pour trouver les inconnues x, y, z :

Sa solution : x = 2, y = -1, z = 1. Donc, a = 2e 1 – e 2 + e 3 = (2,-1,1).

Décomposition vectorielle. Produit scalaire de vecteurs.

Produit scalaire Parfois produit intérieur- opération sur deux vecteurs, dont le résultat est le nombre ( scalaire), indépendant du système de coordonnées et caractérisant les longueurs des vecteurs facteurs et l'angle entre eux. Cette opération correspond à la multiplication longueur vecteur x sur projection vecteur y au vecteur x. Cette opération est généralement considérée comme commutatif Et linéaire pour chaque facteur.

Généralement, l'une des notations suivantes est utilisée :

ou ( désignation Dirac, souvent utilisé dans mécanique quantique pour les vecteurs d'état) :

On suppose généralement que le produit scalaire est défini positif, c'est-à-dire

Pour tout le monde.

Si cela n'est pas supposé, alors le travail est appelé indéfini.

Produit scalaire V espace vectoriel sur champ complexe(ou réel) Nombres est une fonction d'éléments prenant des valeurs dans (ou) définies pour chaque paire d'éléments et satisfaisant les conditions suivantes :

Notez qu'il ressort du paragraphe 2 de la définition que . Par conséquent, le point 3 a du sens, malgré les valeurs complexes (dans le cas général) produit scalaire.

Produit croisé de vecteurs.

Oeuvre vectorielle- Ce pseudovecteur, perpendiculaire plan construit à partir de deux facteurs, qui est le résultat opération binaire"multiplication vectorielle" terminée vecteurs en trois dimensions Espace euclidien. Le travail n'est ni commutatif, ni l'un ni l'autre associatif(c'est anticommutatif) et diffère de produit scalaire de vecteurs. Dans de nombreux problèmes d'ingénierie et de physique, vous devez être capable de construire un vecteur perpendiculaire à deux vecteurs existants - le produit vectoriel offre cette opportunité. Le produit vectoriel est utile pour "mesurer" la perpendiculaire des vecteurs - la longueur du produit vectoriel de deux vecteurs est égale au produit de leurs longueurs s'ils sont perpendiculaires, et diminue jusqu'à zéro si les vecteurs sont parallèles ou antiparallèles.

Le produit vectoriel peut être défini de différentes manières, et théoriquement, dans un espace de n'importe quelle dimension n tu peux calculer le produit n-1 vecteurs, obtenant un seul vecteur perpendiculaire à tous. Mais si le produit est limité à des produits binaires non triviaux avec des résultats vectoriels, alors le produit vectoriel traditionnel n'est défini qu'en trois dimensions et en sept dimensions espaces. Le résultat d'un produit vectoriel, comme d'un produit scalaire, dépend de métrique Espace euclidien.

Contrairement à la formule de calcul à partir de coordonnées vectorielles produit scalaire en trois dimensions système de coordonnées rectangulaires, la formule du produit vectoriel dépend de orientation système de coordonnées rectangulaires ou, en d’autres termes, son « chiralité».

Produit mixte de vecteurs

Produit mixte vecteurs - produit scalaire vecteur sur produit vectoriel vecteurs Et :

On l'appelle parfois produit triple scalaire vecteurs, apparemment dû au fait que le résultat est scalaire(plus précisément - pseudoscalaire).

Signification géométrique : Le module du produit mélangé est numériquement égal au volume parallélépipède, instruit vecteurs .

Travail mixte asymétrique par rapport à tous ses arguments :

c'est-à-dire que la réorganisation de deux facteurs modifie le signe du produit. Il s'ensuit que

En particulier,

Une œuvre mixte peut être facilement écrite en utilisant Symbole Levi-Civita (tenseur):

(dans la dernière formule dans une base orthonormée, tous les indices peuvent être écrits comme des indices inférieurs ; dans ce cas, cette formule répète complètement directement la formule avec le déterminant, cependant, dans ce cas, un multiplicateur (-1) est automatiquement obtenu pour le bases gauche).

Système de coordonnées rectangulaires cartésiennes sur un plan.

Prenons deux droites mutuellement perpendiculaires sur le plan - deux axes de coordonnées Ox et Oy avec les directions positives indiquées dessus (Fig. 1). Les droites Ox et Oy sont appelées axes de coordonnées, le point de leur intersection O est l'origine des coordonnées.

Les axes de coordonnées Ox, Oy avec l'unité d'échelle sélectionnée sont appelés système de coordonnées cartésiennes rectangulaires (ou rectangulaires) sur le plan.

Attribuons deux nombres à un point arbitraire M du plan : l'abscisse x, égale à la distance du point M à l'axe Oy, prise avec le signe « + » si M est à droite de Oy, et avec le Signe « - » si M se trouve à gauche de Oy ; Ordonnée y, égale à la distance du point M à l'axe Ox, prise avec le signe « + » si M est au-dessus de Ox, et avec le signe « - » si M est au-dessous de Ox. L'abscisse x et l'ordonnée y sont appelées coordonnées rectangulaires cartésiennes du point M(x;y).

L'origine a les coordonnées (0;0). Les axes de coordonnées divisent le plan en quatre parties appelées quarts ou quadrants (parfois également appelés angles de coordonnées). La partie du plan comprise entre les demi-axes positifs Ox et Oy est appelée le premier quadrant. Ensuite, les quadrants sont numérotés dans le sens inverse des aiguilles d'une montre (Fig. 2). Pour tous les points du premier quadrant x>0, y>0 ; pour les points I du quadrant x<0, у>0, dans I I I quadrant x<0, у<0 и в IV квадранте х>0, oui<0.

Coordonnées polaires.

Système de coordonnées polaires- un système de coordonnées bidimensionnel dans lequel chaque point du plan est défini par deux nombres : l'angle polaire et le rayon polaire. Le système de coordonnées polaires est particulièrement utile dans les cas où les relations entre les points sont plus facilement représentées en termes de rayons et d'angles ; dans le plus courant cartésien ou un système de coordonnées rectangulaires, de telles relations ne peuvent être établies qu'en appliquant trigonométriqueéquations.

Le système de coordonnées polaires est défini par un rayon, appelé axe zéro ou axe polaire. Le point d’où émerge ce rayon est appelé l’origine ou pôle. Tout point du plan est défini par deux coordonnées polaires : radiale et angulaire. La coordonnée radiale (généralement notée ) correspond à la distance d'un point à l'origine. Coordonnée angulaire, également appelée angle polaire ou azimut et est noté , est égal à l'angle dont l'axe polaire doit être tourné dans le sens inverse des aiguilles d'une montre pour arriver à ce point.

La coordonnée radiale ainsi définie peut prendre des valeurs de zéroà infini, et la coordonnée angulaire varie de 0° à 360°. Cependant, pour plus de commodité, la plage de valeurs de la coordonnée polaire peut être étendue au-delà

Équation d'une droite sur un plan

Définition. Toute droite sur le plan peut être spécifiée par une équation du premier ordre

Hache + Wu + C = 0,

De plus, les constantes A et B ne sont pas égales à zéro en même temps. Cette équation du premier ordre s’appelle équation générale d'une droite. En fonction des valeurs des constantes A, B et C, les cas particuliers suivants sont possibles :

C = 0, A ≠0, B ≠ 0 – la droite passe par l'origine

A = 0, B ≠0, C ≠0 (By + C = 0) - droite parallèle à l'axe Ox

B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – droite parallèle à l'axe Oy

B = C = 0, A ≠0 – la droite coïncide avec l'axe Oy

A = C = 0, B ≠0 – la droite coïncide avec l'axe Ox

L'équation d'une droite peut être présentée sous différentes formes en fonction de conditions initiales données.

Les principales tâches d'utilisation de l'équation d'une droite

je ne peux pas répondre

Courbes du second ordre

Courbe du deuxième ordre- lieu géométrique des points dont les coordonnées rectangulaires cartésiennes satisfont une équation de la forme

dans lequel au moins un des coefficients est différent de zéro.

Limite de séquence de numéros et de fonction

Limite de séquence de numéros. Considérons une séquence de nombres dont le terme commun se rapproche d'un nombre un augmenter le numéro de série n. Dans ce cas, on dit que la séquence de nombres a limite. Ce concept a une définition plus stricte.

Cette définition signifie que un Il y a limite séquence de nombres si son terme commun s'approche sans limite un avec une augmentation n. Géométriquement, cela signifie que pour tout > 0 on peut trouver un tel nombre N qu'à partir de n > N tous les membres de la séquence sont situés à l’intérieur de l’intervalle ( un un). Une suite ayant une limite est appelée convergent; sinon - divergent.

La séquence s'appelle limité, si un tel numéro existe M quoi | toi n | M  pour tout le monde n . Une suite croissante ou décroissante est appelée monotone.

Théorèmes de base sur les limites et leurs applications

Théorème 1 . (sur le passage à la limite dans l'égalité) Si deux fonctions prennent les mêmes valeurs au voisinage d'un certain point, alors leurs limites en ce point coïncident.

Théorème 2. (sur le passage à la limite des inégalités) Si les valeurs de la fonction f(x) au voisinage d'un certain point ne dépassez pas les valeurs correspondantes de la fonction g(x) , alors la limite de la fonction f(x) à ce stade, ne dépasse pas la limite de la fonction g(x) .

Théorème 3 . La limite d’une constante est égale à la constante elle-même.

Preuve. f(x)=c, prouvons cela .

Prenons un >0 arbitraire. Comme  vous pouvez prendre n'importe quel

nombre positif. Puis à

Théorème 4. Fonction ne peut pas avoir deux limites différentes dans

un point.

Preuve. Supposons le contraire. Laisser

Et .

Par le théorème sur le lien entre la limite et la fonction infinitésimale:

f(x)- UN= - b.m. à ,

f(x)- B= - b.m. à .

En soustrayant ces égalités, on obtient :

B-UN= - .

En passant aux limites des deux côtés de l’égalité en , on a :

B-UN=0, c'est-à-dire B=UN. On obtient une contradiction qui prouve le théorème.

Théorème 5. Si chaque terme d'une somme algébrique de fonctions a une limite en , alors la somme algébrique a également une limite en , et la limite de la somme algébrique est égale à la somme algébrique des limites.

.

Preuve. Laisser , , .

Puis, par théorème sur la connexion entre la limite et b.m. fonctions:

Où - b.m. à .

Ajoutons algébriquement ces égalités :

f(x)+ g(x)- h(x)-(A+B-C)= ,

Où b.m. à .

D'après le théorème sur le lien entre la limite et b.m. Caractéristiques:

A+B-C= .

Théorème 6. Si chacun des facteurs d'un produit d'un nombre fini de fonctions a une limite en , alors le produit a également une limite en , et la limite du produit est égale au produit des limites.

.

Conséquence. Le facteur constant peut être pris au-delà du signe limite.

.

Théorème 7. Si les fonctions f(x) Et g(x) avoir une limite à ,

et , alors leur quotient a aussi une limite en , et la limite du quotient est égale au quotient des limites.

, .

Continuité de fonction

Sur la fig. 15, et le graphique de la fonction est affiché . Il est naturel de l’appeler un graphique continu car il peut être dessiné d’un seul mouvement de crayon sans le retirer du papier. Fixons un point (nombre) arbitraire. Un autre point proche peut être écrit sous la forme , où se trouve un nombre positif ou négatif appelé incrément. Différence

est appelé l'incrément de la fonction au point correspondant à l'incrément. Ce que l'on veut dire ici, c'est que . Sur la fig. 15, et est égale à la longueur du segment.

Nous nous efforcerons d’atteindre zéro ; alors pour la fonction en question, elle tendra évidemment vers zéro :

. (1)

Considérons maintenant le graphique de la Fig. 15, b. Il se compose de deux pièces continues et. Cependant, ces éléments ne sont pas continuellement connectés et il est donc naturel de qualifier le graphique de discontinu. Pour que le graphique représente une fonction à valeur unique au point , convenons qu'elle est égale à la longueur du segment reliant et ; en signe de cela, le point est représenté sur le graphique par un cercle, tandis que le point est représenté par une flèche indiquant qu'il n'appartient pas au graphique. Si le point appartenait au graphique, alors la fonction aurait deux valeurs au point.

Ajoutons maintenant un incrément et déterminons l'incrément correspondant de la fonction :

Si nous tendons vers zéro, nous ne pouvons plus dire ce qui tendra vers zéro. Pour les négatifs tendant vers zéro, cela est vrai, mais pour les positifs ce n'est pas du tout le cas : d'après la figure, il est clair que si, tout en restant positif, tend vers zéro, alors l'incrément correspondant tend vers un nombre positif égal à la longueur du segment.

Après ces considérations, il est naturel d'appeler une fonction définie sur un intervalle continu en un point de ce segment si son incrément en ce point, correspondant à l'incrément, tend vers zéro de quelque manière qu'il tend vers zéro. Ceci (la propriété de continuité dans) s'écrit sous la forme de la relation (1) ou aussi comme ceci :

L'entrée (2) se lit comme ceci : la limite est égale à zéro lorsqu'elle tend vers zéro selon n'importe quelle loi. Cependant, l'expression « conformément à toute loi » est généralement omise, ce qui le sous-entend.

Si une fonction définie sur n'est pas continue au point , c'est-à-dire si la propriété (2) ne s'applique pas à elle dans au moins une manière de tendre vers zéro, alors elle est dite discontinue au point .

La fonction représentée sur la Fig. 15, a, est continue en tout point, mais la fonction représentée sur la Fig. 15, b, évidemment, est continue en tout point, à l'exception du point, car pour ce dernier, la relation (2) n'est pas satisfaite lorsque, restant positive.

Une fonction continue en tout point sur un segment (intervalle) est appelée continue sur ce segment (intervalle).

Une fonction continue exprime mathématiquement une propriété que l'on rencontre souvent en pratique, à savoir qu'un petit incrément dans une variable indépendante correspond à un petit incrément dans une variable dépendante (fonction). D'excellents exemples de fonction continue sont diverses lois du mouvement des corps, exprimant la dépendance du chemin parcouru par le corps au temps. Le temps et l'espace sont continus. Telle ou telle loi du mouvement établit entre elles une certaine connexion continue, caractérisée par le fait qu'à un petit incrément de trajet correspond un petit incrément de temps.

L'homme est parvenu à l'abstraction de la continuité en observant les milieux dits continus qui l'entourent - solides, liquides ou gazeux, par exemple les métaux, l'eau, l'air. En fait, tout milieu physique est une accumulation d’un grand nombre de particules en mouvement séparées les unes des autres. Cependant, ces particules et les distances qui les séparent sont si petites par rapport aux volumes de milieu que nous devons traiter dans les phénomènes physiques macroscopiques que bon nombre de ces phénomènes peuvent être assez bien étudiés si l'on considère approximativement que la masse du milieu étudié est distribué en continu sans aucune lacune dans l'espace qu'il occupe. De nombreuses disciplines physiques sont basées sur cette hypothèse, par exemple l'hydrodynamique, l'aérodynamique et la théorie de l'élasticité. Le concept mathématique de continuité joue naturellement un rôle important dans ces disciplines, comme dans bien d’autres.

Les fonctions continues constituent la principale classe de fonctions avec lesquelles opère l'analyse mathématique.

Des exemples de fonctions continues sont les fonctions élémentaires (voir § 3.8 ci-dessous). Ils sont continus sur les intervalles de changement où ils sont définis.

Les fonctions discontinues en mathématiques reflètent les processus discontinus trouvés dans la nature. Lors d’un impact par exemple, la vitesse d’un corps change brusquement. De nombreuses transitions de qualité s'accompagnent de sauts. Par exemple, la relation entre la température d'un gramme d'eau (glace) et la quantité de calories de chaleur qu'il contient, lorsqu'elle varie entre et , si l'on suppose classiquement qu'avec la valeur de , est exprimée par les formules suivantes :

Nous supposons que la capacité thermique de la glace est de 0,5. Lorsque cette fonction s'avère indéfinie – multi-valuée ; Pour plus de commodité, nous pouvons convenir qu'il prend une valeur bien définie, par exemple . La fonction, évidemment discontinue en , est représentée sur la Fig. 16.

Définissons la continuité d'une fonction en un point.

Une fonction est dite continue en un point si elle est définie dans un certain voisinage de ce point, y compris au point lui-même, et si son incrément en ce point, correspondant à l'incrément de l'argument, tend vers zéro en :

Si l'on met , on obtient la définition équivalente suivante de la continuité en : une fonction est continue en un point si elle est définie dans un voisinage de ce point, y compris au point lui-même, et si

; (4)

ou encore dans la langue : si pour tout le monde il y a tel que

L'égalité (4) peut également s'écrire comme suit :

. (4’)

Il montre que sous le signe d'une fonction continue on peut aller à la limite.

Exemple 1. Une constante est une fonction continue en tout point. En fait, un point correspond à la valeur d'une fonction, un point correspond à la même valeur . Donc

.

EXEMPLE 2. La fonction est continue pour n'importe quelle valeur car et, donc, pour .

Exemple 3. La fonction est continue pour tout . En fait,

Mais pour tout le monde il y a des inégalités

Si , alors cela découle de la Fig. 17, qui montre un cercle de rayon 1 (l'arc de longueur est plus grand que la corde qu'il sous-tend, qui a une longueur ). Quand l’inégalité (6) se transforme en égalité. Si alors . Enfin, si , alors . De (5) basé sur (6) il résulte

,

Mais alors évidemment

On peut aussi dire que pour tout le monde il est possible de trouver exactement tel que

Notons un théorème important.

Théorème 1. Si les fonctions et sont continues en un point, alors leur somme, leur différence, leur produit et leur quotient (at) sont également continus en ce point.

Ce théorème découle directement du théorème 6 §3.2, en tenant compte du fait que dans ce cas

Un théorème important sur la continuité d'une fonction à partir d'une fonction (fonction complexe) est également vrai.

Théorème 2. Soit une fonction continue au point , et une autre fonction continue au point , et soit . Alors la fonction complexe est continue au point.

Preuve. Notez que par la définition de la continuité d'une fonction en un point, il s'ensuit qu'elle est définie dans un certain voisinage de ce point. C'est pourquoi

Ici, une substitution est introduite et la continuité au point est prise en compte .

Exemple 4. Fonction

où sont des coefficients constants, est appelé polynôme de degré. C’est continu pour tout le monde. Après tout, pour obtenir, il est nécessaire, sur la base de nombres constants et de fonctions, d'effectuer un nombre fini d'opérations arithmétiques - addition, soustraction et multiplication. Mais une constante est une fonction continue (voir exemple 1), et une fonction est également continue (voir exemple 2), donc la continuité découle du théorème 1.

Exemple 5. La fonction est continue. C'est une composition de deux fonctions continues : , .

Exemple 6. Fonction

est continu pour le spécifié, car (voir Théorème 1) il est égal au quotient de la division des fonctions continues et le diviseur n'est pas égal à zéro (pour le spécifié).

Exemple 7. Fonction

est continue pour tout , car c'est une composition de fonctions continues : , , (voir Théorème 2).

Exemple 8. La fonction est continue car

Exemple 9. Si une fonction est continue en un point, alors la fonction est également continue en ce point.

Cela découle du théorème 2 et de l'exemple 8, car une fonction est une composition de deux fonctions continues, .

Notons deux autres théorèmes qui découlent directement des théorèmes correspondants 1 et 2 du §3.2 pour la limite d'une fonction.

Théorème 3. Si une fonction est continue en un point, alors il existe un voisinage de ce point auquel elle est bornée.

Théorème 4. Si la fonction est continue au point et , alors il existe un voisinage du point auquel

.

De plus, si , alors

et si, alors

Le concept de dérivé.

Dérivé(fonctionne en un point) - concept de base calcul différentiel, caractérisant le taux de changement de la fonction (à un point donné). Défini comme limite la relation entre l'incrément d'une fonction et son incrément argument lorsque l'incrément de l'argument tend à zéro, si une telle limite existe. Une fonction qui a une dérivée finie (à un moment donné) est appelée différentiable (à ce stade).

Le processus de calcul de la dérivée est appelé différenciation. Processus inverse - découverte primitive - intégration.

Signification géométrique et mécanique des dérivées.

Règles de différenciation.

Dérivée d'une somme algébrique de fonctions

Théorème 1. Dérivé la somme (différence) de deux fonctions différentiables est égale à la somme (différence) des dérivées de ces fonctions :

(u±v)" = u"±v"

Conséquence. La dérivée d'une somme algébrique finie de fonctions différentiables est égale à la même somme algébrique de dérivées de termes. Par exemple,

(u - v + w)" = u" - v" + w"

La dérivée du produit des fonctions est déterminée par

Théorème 2. La dérivée du produit de deux fonctions différentiables est égale au produit de la première fonction et de la dérivée de la seconde plus le produit de la deuxième fonction et de la dérivée de la première, c'est-à-dire

(uv)" = u"v + uv"

Corollaire 1. Le facteur constant peut être soustrait du signe de la dérivée (cv)" = cv" (c = const).

Corollaire 2. La dérivée du produit de plusieurs fonctions différentiables est égale à la somme des produits de la dérivée de chacune d'elles par toutes les autres.

Par exemple, (uvw)" = u"vw + uv"w + uvw"

Dérivée du quotient de deux fonctions

est exprimé par le théorème suivant.

Théorème 3. La dérivée du quotient de deux fonctions différentiables est déterminée par la formule

La dérivée d'une fonction complexe s'exprime par

Théorème 4. Si y = f(u) et u = (ф(x)) sont des fonctions différentiables de leurs arguments, alors dérivée d'une fonction complexe y = f (ф(x)) existe et est égal au produit de la dérivée de cette fonction par rapport à l'argument intermédiaire et de la dérivée de l'argument intermédiaire par rapport à la variable indépendante, c'est-à-dire

Très souvent dans tests de mathématiques sur les dérivées des fonctions complexes sont données, par exemple y = sin(cos5x). La dérivée d'une telle fonction est égale à -5sin5x*sin(cos5x)

Voir un exemple de calcul d'une fonction complexe dans la vidéo suivante

Dérivées de fonctions élémentaires.

Dérivées de fonctions élémentaires d'un argument simple	Fonctionoui = f (kx +b )	Dérivées de fonctions élémentaires d'un argument complexe
oui=xn	oui=nxn−1	oui=(kx+b)n	oui=nk(kx+b)n−1
		oui=(kx+b)

Niveau d'entrée

Dérivée d'une fonction. Le guide ultime (2019)

Imaginons une route droite traversant une zone vallonnée. Autrement dit, il monte et descend, mais ne tourne ni à droite ni à gauche. Si l'axe est dirigé horizontalement le long de la route et verticalement, alors la ligne de route sera très similaire au graphique d'une fonction continue :

L'axe est un certain niveau d'altitude zéro ; dans la vie, nous utilisons le niveau de la mer comme tel.

À mesure que nous avançons sur une telle route, nous montons ou descendons également. On peut aussi dire : lorsque l'argument change (déplacement le long de l'axe des abscisses), la valeur de la fonction change (déplacement le long de l'axe des ordonnées). Réfléchissons maintenant à la façon de déterminer la « raideur » de notre route ? Quel genre de valeur cela pourrait-il représenter ? C'est très simple : à quel point la hauteur va changer en avançant sur une certaine distance. En effet, sur différents tronçons de route, en avançant (le long de l'axe des x) d'un kilomètre, nous monterons ou descendrons d'un nombre différent de mètres par rapport au niveau de la mer (le long de l'axe des y).

Notons la progression (lire « delta x »).

La lettre grecque (delta) est couramment utilisée en mathématiques comme préfixe signifiant « changement ». C'est-à-dire - c'est un changement de quantité, - un changement ; alors qu'est-ce que c'est ? C'est vrai, un changement d'ampleur.

Important : une expression est un tout unique, une variable. Ne séparez jamais le « delta » du « x » ou de toute autre lettre !

C'est par exemple .

La valeur est facile à calculer : si au début nous étions en hauteur, et qu'après le déplacement nous nous retrouvions en hauteur, alors. Si le point final est inférieur au point de départ, il sera négatif - cela signifie que nous ne montons pas, mais descendons.

Revenons à la « raideur » : c'est une valeur qui montre de combien (forte) la hauteur augmente lorsque l'on avance d'une unité de distance :

Supposons que sur une section de la route, en avançant d'un kilomètre, la route s'élève d'un kilomètre. Alors la pente à cet endroit est égale. Et si la route, en avançant de m, descendait de km ? Alors la pente est égale.

Regardons maintenant le sommet d'une colline. Si vous prenez le début du tronçon un demi-kilomètre avant le sommet et la fin un demi-kilomètre après, vous constaterez que la hauteur est presque la même.

Autrement dit, selon notre logique, il s'avère que la pente ici est presque égale à zéro, ce qui n'est clairement pas vrai. Sur une distance de plusieurs kilomètres, beaucoup de choses peuvent changer. Il est nécessaire de considérer des zones plus petites pour une évaluation plus adéquate et plus précise de la pente. Par exemple, si vous mesurez le changement de hauteur lorsque vous vous déplacez d’un mètre, le résultat sera beaucoup plus précis. Mais même cette précision peut ne pas nous suffire - après tout, s'il y a un poteau au milieu de la route, nous pouvons simplement le dépasser. Quelle distance choisir alors ? Centimètre? Millimètre? Moins c'est plus !

Dans la vraie vie, mesurer les distances au millimètre près est largement suffisant. Mais les mathématiciens recherchent toujours la perfection. Le concept a donc été inventé infinitésimal, c’est-à-dire que la valeur absolue est inférieure à n’importe quel nombre que nous pouvons nommer. Par exemple, vous dites : un billionième ! Combien moins ? Et vous divisez ce nombre par - et ce sera encore moins. Et ainsi de suite. Si on veut écrire qu’une quantité est infinitésimale, on écrit ainsi : (on lit « x tend vers zéro »). Il est très important de comprendre que ce nombre n'est pas égal à zéro ! Mais très proche. Cela signifie que vous pouvez diviser par cela.

Le concept opposé à infinitésimal est infiniment grand (). Vous l'avez probablement déjà rencontré lorsque vous travailliez sur les inégalités : ce nombre est modulo supérieur à tous les nombres auxquels vous pouvez penser. Si vous obtenez le plus grand nombre possible, multipliez-le simplement par deux et vous obtiendrez un nombre encore plus grand. Et l’infini est encore plus grand que ce qui arrive. En fait, l'infiniment grand et l'infiniment petit sont l'inverse l'un de l'autre, c'est-à-dire at, et vice versa : at.

Revenons maintenant à notre route. La pente idéalement calculée est la pente calculée pour un segment infinitésimal du chemin, soit :

Je constate qu'avec un déplacement infinitésimal, le changement de hauteur sera également infinitésimal. Mais permettez-moi de vous rappeler qu'infinitésimal ne signifie pas égal à zéro. Si vous divisez des nombres infinitésimaux les uns par les autres, vous pouvez obtenir un nombre tout à fait ordinaire, par exemple . Autrement dit, une petite valeur peut être exactement plusieurs fois supérieure à une autre.

A quoi ça sert tout ça ? La route, la pente... Nous ne participons pas à un rallye automobile, mais nous enseignons les mathématiques. Et en mathématiques, tout est exactement pareil, seulement appelé différemment.

Notion de dérivé

La dérivée d'une fonction est le rapport de l'incrément de la fonction à l'incrément de l'argument pour un incrément infinitésimal de l'argument.

Progressivement en mathématiques, ils appellent le changement. La mesure dans laquelle l'argument () change à mesure qu'il se déplace le long de l'axe est appelée incrément d'argument et est désigné dans quelle mesure la fonction (hauteur) a changé lors du déplacement vers l'avant le long de l'axe d'une distance est appelé. incrément de fonction et est désigné.

Ainsi, la dérivée d’une fonction est le rapport au quand. On note la dérivée par la même lettre que la fonction, seulement avec un nombre premier en haut à droite : ou simplement. Écrivons donc la formule dérivée en utilisant ces notations :

Comme dans l'analogie avec la route, ici lorsque la fonction augmente, la dérivée est positive, et lorsqu'elle diminue, elle est négative.

La dérivée peut-elle être égale à zéro ? Certainement. Par exemple, si nous roulons sur une route horizontale et plate, la pente est nulle. Et c’est vrai, la hauteur ne change pas du tout. Il en est de même de la dérivée : la dérivée d'une fonction constante (constante) est égale à zéro :

puisque l'incrément d'une telle fonction est égal à zéro pour tout.

Rappelons-nous l'exemple du sommet d'une colline. Il s'est avéré qu'il était possible de disposer les extrémités du segment sur les côtés opposés du sommet de manière à ce que la hauteur aux extrémités soit la même, c'est-à-dire que le segment soit parallèle à l'axe :

Mais de grands segments sont le signe d’une mesure inexacte. Nous élèverons notre segment parallèlement à lui-même, puis sa longueur diminuera.

Finalement, lorsque nous serons infiniment proches du sommet, la longueur du segment deviendra infinitésimale. Mais en même temps, il est resté parallèle à l'axe, c'est-à-dire que la différence de hauteur à ses extrémités est égale à zéro (elle ne tend pas vers, mais est égale à). Donc la dérivée

Cela peut être compris ainsi : lorsque nous nous trouvons tout en haut, un petit déplacement vers la gauche ou la droite modifie de manière négligeable notre hauteur.

Il existe aussi une explication purement algébrique : à gauche du sommet la fonction augmente, et à droite elle diminue. Comme nous l’avons découvert précédemment, lorsqu’une fonction augmente, la dérivée est positive, et lorsqu’elle diminue, elle est négative. Mais cela change en douceur, sans sauts (puisque la route ne change brusquement de pente nulle part). Il doit donc y avoir une différence entre les valeurs négatives et positives. Ce sera là où la fonction n'augmente ni ne diminue - au point sommet.

Il en va de même pour le creux (la zone où la fonction à gauche diminue et à droite augmente) :

Un peu plus sur les incréments.

Nous changeons donc l’argument en grandeur. On change à partir de quelle valeur ? Qu’est-il devenu (l’argument) maintenant ? Nous pouvons choisir n'importe quel point, et maintenant nous allons danser à partir de lui.

Considérons un point avec une coordonnée. La valeur de la fonction qu'il contient est égale. Ensuite on fait le même incrément : on augmente la coordonnée de. Quel est l’argument maintenant ? Très simple : . Quelle est la valeur de la fonction maintenant ? Là où va l’argument, la fonction aussi : . Qu'en est-il de l'incrément de fonction ? Rien de nouveau : c'est toujours l'ampleur de l'évolution de la fonction :

Entraînez-vous à trouver des incréments :

1. Recherchez l'incrément de la fonction à un point où l'incrément de l'argument est égal à.
2. Il en va de même pour la fonction en un point.

Solutions :

À différents points avec le même incrément d'argument, l'incrément de fonction sera différent. Cela signifie que la dérivée en chaque point est différente (nous en avons discuté au tout début - la pente de la route est différente en différents points). Ainsi, lorsque l’on écrit une dérivée, il faut indiquer à quel moment :

Fonction de puissance.

Une fonction puissance est une fonction dont l’argument est dans une certaine mesure (logique, n’est-ce pas ?).

De plus - dans une certaine mesure : .

Le cas le plus simple est celui où l'exposant est :

Trouvons sa dérivée en un point. Rappelons la définition d'une dérivée :

L’argument change donc de à. Quel est l'incrément de la fonction ?

L'incrément, c'est ça. Mais une fonction est en tout point égale à son argument. C'est pourquoi :

La dérivée est égale à :

La dérivée de est égale à :

b) Considérons maintenant la fonction quadratique () : .

Maintenant, rappelons-le. Cela signifie que la valeur de l'incrément peut être négligée, puisqu'elle est infinitésimale, et donc insignifiante par rapport à l'autre terme :

Nous avons donc proposé une autre règle :

c) On continue la série logique : .

Cette expression peut être simplifiée de différentes manières : ouvrez la première parenthèse en utilisant la formule de multiplication abrégée du cube de la somme, ou factorisez l'expression entière en utilisant la formule de différence des cubes. Essayez de le faire vous-même en utilisant l'une des méthodes suggérées.

J'ai donc obtenu ceci :

Et encore une fois, rappelons-le. Cela signifie que l'on peut négliger tous les termes contenant :

On obtient : .

d) Des règles similaires peuvent être obtenues pour les grandes puissances :

e) Il s'avère que cette règle peut être généralisée pour une fonction puissance avec un exposant arbitraire, pas même un entier :

(2)

La règle peut être formulée ainsi : « le diplôme est avancé sous forme de coefficient, puis diminué de . »

Nous prouverons cette règle plus tard (presque à la toute fin). Voyons maintenant quelques exemples. Trouvez la dérivée des fonctions :

1. (de deux manières : par formule et en utilisant la définition de dérivée - en calculant l'incrément de la fonction) ;

1. . Croyez-le ou non, il s’agit d’une fonction de pouvoir. Si vous avez des questions comme « Comment ça va ? Où est le diplôme ? », souvenez-vous du sujet « » !
   Oui, oui, la racine est aussi un degré, uniquement fractionnaire : .
   Cela signifie que notre racine carrée n’est qu’une puissance avec un exposant :
   .
   Nous recherchons la dérivée en utilisant la formule récemment apprise :

   Si à ce stade cela devient à nouveau flou, répétez le sujet « » !!! (environ un degré avec un exposant négatif)

2. . Maintenant l'exposant :

   Et maintenant à travers la définition (vous avez déjà oublié ?) :
   ;
   .
   Maintenant, comme d'habitude, nous négligeons le terme contenant :
   .

3. . Combinaison de cas précédents : .

Fonctions trigonométriques.

Ici, nous utiliserons un fait issu des mathématiques supérieures :

Avec expression.

Vous en apprendrez la preuve dès la première année d'institut (et pour y arriver, vous devez réussir l'examen d'État unifié). Maintenant, je vais juste le montrer graphiquement :

Nous voyons que lorsque la fonction n'existe pas, le point sur le graphique est coupé. Mais plus la valeur est proche, plus la fonction est proche de ce qui « vise ».

De plus, vous pouvez vérifier cette règle à l'aide d'une calculatrice. Oui, oui, ne soyez pas timide, prenez une calculatrice, nous n'en sommes pas encore à l'examen d'État unifié.

Alors, essayons : ;

N'oubliez pas de passer votre calculatrice en mode Radians !

etc. On voit que plus la valeur du rapport est petite, plus la valeur du rapport est proche de.

a) Considérons la fonction. Comme d'habitude, trouvons son incrément :

Transformons la différence des sinus en un produit. Pour ce faire, nous utilisons la formule (rappelez-vous le sujet « ») : .

Maintenant la dérivée :

Faisons un remplacement : . Alors pour infinitésimal c'est aussi infinitésimal : . L'expression pour prend la forme :

Et maintenant, nous nous en souvenons avec l'expression. Et aussi, que se passerait-il si une quantité infinitésimale pouvait être négligée dans la somme (c'est-à-dire at).

On obtient donc la règle suivante : la dérivée du sinus est égale au cosinus:

Ce sont des dérivés basiques (« tabulaires »). Les voici dans une seule liste :

Plus tard, nous leur en ajouterons quelques autres, mais ce sont les plus importants, car ils sont les plus souvent utilisés.

Pratique:

1. Trouver la dérivée de la fonction en un point ;
2. Trouvez la dérivée de la fonction.

Solutions :

1. Tout d'abord, trouvons la dérivée sous forme générale, puis substituons sa valeur :
   ;
   .
2. Nous avons ici quelque chose de similaire à une fonction puissance. Essayons de l'amener à
   vue normale :
   .
   Super, vous pouvez maintenant utiliser la formule :
   .
   .
3. . Eeeeeee….. Qu'est-ce que c'est ????

Bon, vous avez raison, on ne sait pas encore comment trouver de tels dérivés. Nous avons ici une combinaison de plusieurs types de fonctions. Pour travailler avec eux, vous devez apprendre quelques règles supplémentaires :

Exposant et logarithme népérien.

Il existe une fonction en mathématiques dont la dérivée pour toute valeur est à la fois égale à la valeur de la fonction elle-même. C'est ce qu'on appelle « exposant » et c'est une fonction exponentielle.

La base de cette fonction - une constante - est une fraction décimale infinie, c'est-à-dire un nombre irrationnel (comme). On l'appelle le « nombre d'Euler », c'est pourquoi il est désigné par une lettre.

Donc la règle :

Très facile à retenir.

Bon, n’allons pas loin, considérons immédiatement la fonction inverse. Quelle fonction est l'inverse de la fonction exponentielle ? Logarithme:

Dans notre cas, la base est le nombre :

Un tel logarithme (c'est-à-dire un logarithme avec une base) est appelé « naturel », et nous utilisons pour cela une notation spéciale : nous l'écrivons à la place.

A quoi est-ce égal ? Bien sûr.

La dérivée du logarithme népérien est également très simple :

Exemples :

1. Trouvez la dérivée de la fonction.
2. Quelle est la dérivée de la fonction ?

Réponses : Les logarithmes exponentiel et naturel sont des fonctions particulièrement simples du point de vue dérivé. Les fonctions exponentielles et logarithmiques avec n'importe quelle autre base auront une dérivée différente, que nous analyserons plus tard, après avoir parcouru les règles de différenciation.

Règles de différenciation

Des règles de quoi ? Encore un nouveau terme, encore ?!...

Différenciation est le processus de recherche de la dérivée.

C'est tout. Comment pouvez-vous appeler ce processus en un mot ? Pas dérivé... Les mathématiciens appellent la différentielle le même incrément d'une fonction à. Ce terme vient du latin différentia – différence. Ici.

Lors de la dérivation de toutes ces règles, nous utiliserons deux fonctions, par exemple et. Nous aurons également besoin de formules pour leurs incréments :

Il y a 5 règles au total.

La constante est soustraite du signe dérivé.

Si - un nombre constant (constant), alors.

Évidemment, cette règle fonctionne aussi pour la différence : .

Prouvons-le. Laissez-le être, ou plus simple.

Exemples.

Trouvez les dérivées des fonctions :

1. à un moment donné ;
2. à un moment donné ;
3. à un moment donné ;
4. au point.

Solutions :

1. (la dérivée est la même en tous points, puisque c'est une fonction linéaire, vous vous souvenez ?) ;

Dérivé du produit

Tout est similaire ici : introduisons une nouvelle fonction et trouvons son incrément :

Dérivé:

Exemples :

1. Trouver les dérivées des fonctions et ;
2. Trouvez la dérivée de la fonction en un point.

Solutions :

Dérivée d'une fonction exponentielle

Vos connaissances sont désormais suffisantes pour apprendre à trouver la dérivée de n'importe quelle fonction exponentielle, et pas seulement les exposants (avez-vous déjà oublié ce que c'est ?).

Alors, où est un certain nombre.

Nous connaissons déjà la dérivée de la fonction, essayons donc de réduire notre fonction à une nouvelle base :

Pour ce faire, nous utiliserons une règle simple : . Alors:

Eh bien, ça a fonctionné. Essayez maintenant de trouver la dérivée, et n'oubliez pas que cette fonction est complexe.

Est-ce que ça a marché ?

Ici, vérifiez par vous-même :

La formule s'est avérée très similaire à la dérivée d'un exposant : telle qu'elle était, elle reste la même, seul un facteur est apparu, qui n'est qu'un nombre, mais pas une variable.

Exemples :
Trouvez les dérivées des fonctions :

Réponses :

Il s'agit simplement d'un nombre qui ne peut pas être calculé sans calculatrice, c'est-à-dire qu'il ne peut pas être écrit sous une forme plus simple. Par conséquent, nous le laissons sous cette forme dans la réponse.

Dérivée d'une fonction logarithmique

C’est pareil ici : vous connaissez déjà la dérivée du logarithme népérien :

Par conséquent, pour trouver un logarithme arbitraire avec une base différente, par exemple :

Nous devons réduire ce logarithme à la base. Comment changer la base d'un logarithme ? J'espère que vous vous souvenez de cette formule :

Seulement maintenant, nous écrirons à la place :

Le dénominateur est simplement une constante (un nombre constant, sans variable). La dérivée s’obtient très simplement :

Les dérivées des fonctions exponentielles et logarithmiques ne sont presque jamais trouvées dans l'examen d'État unifié, mais il ne sera pas superflu de les connaître.

Dérivée d'une fonction complexe.

Qu'est-ce qu'une « fonction complexe » ? Non, ce n'est pas un logarithme, ni une arctangente. Ces fonctions peuvent être difficiles à comprendre (même si si vous trouvez le logarithme difficile, lisez le sujet « Logarithmes » et tout ira bien), mais d'un point de vue mathématique, le mot « complexe » ne signifie pas « difficile ».

Imaginez un petit tapis roulant : deux personnes sont assises et effectuent des actions avec des objets. Par exemple, le premier enveloppe une barre de chocolat dans un emballage et le second l'attache avec un ruban. Le résultat est un objet composite : une barre de chocolat enveloppée et nouée avec un ruban. Pour manger une barre de chocolat, vous devez effectuer les étapes inverses dans l’ordre inverse.

Créons un pipeline mathématique similaire : nous trouverons d'abord le cosinus d'un nombre, puis nous mettrons au carré le nombre obtenu. Donc, on nous donne un nombre (chocolat), je trouve son cosinus (emballage), et puis vous mettez au carré ce que j'ai obtenu (nouez-le avec un ruban). Ce qui s'est passé? Fonction. Ceci est un exemple de fonction complexe : lorsque, pour trouver sa valeur, on effectue une première action directement avec la variable, puis une deuxième action avec ce qui résulte de la première.

On peut facilement faire les mêmes étapes dans l'ordre inverse : on le met d'abord au carré, et je cherche ensuite le cosinus du nombre obtenu : . Il est facile de deviner que le résultat sera presque toujours différent. Une caractéristique importante des fonctions complexes : lorsque l'ordre des actions change, la fonction change.

Autrement dit, une fonction complexe est une fonction dont l'argument est une autre fonction: .

Pour le premier exemple, .

Deuxième exemple : (même chose). .

L'action que nous faisons en dernier sera appelée fonction "externe", et l'action effectuée en premier - en conséquence fonction "interne"(ce sont des noms informels, je les utilise uniquement pour expliquer le matériel dans un langage simple).

Essayez de déterminer par vous-même quelle fonction est externe et laquelle interne :

Réponses : La séparation des fonctions internes et externes est très similaire à la modification de variables : par exemple, dans une fonction

1. Quelle action allons-nous effectuer en premier ? Tout d’abord, calculons le sinus, puis cubez-le seulement. Cela signifie qu’il s’agit d’une fonction interne, mais externe.
   Et la fonction originelle est leur composition : .
2. Interne: ; externe: .
   Examen : .
3. Interne: ; externe: .
   Examen : .
4. Interne: ; externe: .
   Examen : .
5. Interne: ; externe: .
   Examen : .

Nous changeons les variables et obtenons une fonction.

Eh bien, maintenant nous allons extraire notre barre de chocolat et chercher le dérivé. La procédure est toujours inversée : on cherche d’abord la dérivée de la fonction externe, puis on multiplie le résultat par la dérivée de la fonction interne. Par rapport à l'exemple original, cela ressemble à ceci :

Autre exemple :

Alors, formulons enfin la règle officielle :

Algorithme pour trouver la dérivée d'une fonction complexe :

Cela semble simple, non ?

Vérifions avec des exemples :

Solutions :

1) Interne : ;

Externe: ;

2) Interne : ;

(N’essayez pas de le couper maintenant ! Rien ne sort sous le cosinus, vous vous souvenez ?)

3) Interne : ;

Externe: ;

Il est immédiatement clair qu'il s'agit d'une fonction complexe à trois niveaux : après tout, c'est déjà une fonction complexe en soi, et nous en extrayons également la racine, c'est-à-dire que nous effectuons la troisième action (mettre le chocolat dans un emballage et avec un ruban dans la mallette). Mais il n'y a aucune raison d'avoir peur : nous allons quand même « déballer » cette fonction dans le même ordre que d'habitude : depuis la fin.

Autrement dit, nous différencions d'abord la racine, puis le cosinus, et ensuite seulement l'expression entre parenthèses. Et puis on multiplie le tout.

Dans de tels cas, il est pratique de numéroter les actions. Autrement dit, imaginons ce que nous savons. Dans quel ordre effectuerons-nous les actions pour calculer la valeur de cette expression ? Regardons un exemple :

Plus l’action est réalisée tardivement, plus la fonction correspondante sera « externe ». La séquence d'actions est la même que précédemment :

Ici, la nidification est généralement à 4 niveaux. Déterminons la marche à suivre.

1. Expression radicale. .

2. Racine. .

3. Sinus. .

4. Carré. .

5. Rassembler le tout :

DÉRIVÉ. EN BREF SUR LES CHOSES PRINCIPALES

Dérivée d'une fonction- le rapport de l'incrément de la fonction à l'incrément de l'argument pour un incrément infinitésimal de l'argument :

Dérivés de base :

Règles de différenciation :

La constante est soustraite du signe dérivé :

Dérivée de la somme :

Dérivé du produit :

Dérivée du quotient :

Dérivée d'une fonction complexe :

Algorithme pour trouver la dérivée d'une fonction complexe :

1. Nous définissons la fonction « interne » et trouvons sa dérivée.
2. Nous définissons la fonction « externe » et trouvons sa dérivée.
3. Nous multiplions les résultats des premier et deuxième points.

Lors de la résolution de problèmes de différenciation, il faut rechercher des dérivées de fonctions de différentes classes. Dans cet article, nous examinerons les principaux règles de différenciation, que nous utiliserons constamment pour trouver des dérivées. Nous prouverons toutes ces règles à partir de la définition de la dérivée d'une fonction et nous attarderons certainement sur la solution détaillée d'exemples afin de comprendre le principe de leur application.

Lors de la démonstration des règles de différenciation, nous supposerons que les fonctions f(x) et g(x) sont dérivables sur un certain intervalle X.

Autrement dit, pour tout il est vrai que , où sont les incréments des fonctions correspondantes.

Dans un autre post.

Les règles de base de différenciation comprennent :

Réaliser un facteur constant au-delà du signe de la dérivée.

Montrons la formule. Par définition de dérivée on a :

Un facteur arbitraire peut être pris au-delà du signe de passage à la limite (ceci est connu grâce aux propriétés de la limite), donc

Ceci termine la preuve de la première règle de différenciation.

Bien souvent, il est nécessaire de simplifier d'abord la forme de la fonction différentiable afin d'utiliser le tableau des dérivées et les règles de recherche des dérivées. Les exemples suivants le confirment clairement.

Exemple.

Effectuer une différenciation des fonctions .

Solution.

Sur la base des propriétés de la fonction logarithmique, vous pouvez accéder à la notation. Reste à retenir la dérivée de la fonction logarithmique et à ajouter un facteur constant :

Exemple.

Solution.

Transformons la fonction d'origine .

Nous appliquons la règle de placer le multiplicateur en dehors du signe de la dérivée et retirons la dérivée de la fonction exponentielle du tableau :

Dérivée d'une somme, dérivée d'une différence.

Pour prouver la deuxième règle de différenciation, nous utilisons la définition d'une dérivée et la propriété de la limite d'une fonction continue.

De la même manière, on peut prouver que la dérivée de la somme (différence) de n fonctions est égale à la somme (différence) de n dérivées.

Exemple.

Trouver la dérivée d'une fonction .

Solution.

Simplifions la forme de la fonction d'origine.

Nous utilisons la règle de la somme dérivée (différence) :

Dans le paragraphe précédent, nous avons prouvé que le facteur constant peut être soustrait du signe de la dérivée, donc

Il ne reste plus qu'à utiliser la table des dérivées :

Dérivée du produit de fonctions.

Démontrons la règle pour différencier le produit de deux fonctions.

Écrivons la limite du rapport de l'incrément d'un produit de fonctions à l'incrément de l'argument. Nous prendrons en compte cela et (l'incrément de la fonction tend vers zéro comme l'incrément de l'argument tend vers zéro).

Q.E.D.

Exemple.

Fonction différenciée .

Solution.

Dans cet exemple. Nous appliquons la règle de dérivée du produit :

Nous nous tournons vers le tableau des dérivées des fonctions élémentaires de base et obtenons la réponse :

Exemple.

Trouvez la dérivée de la fonction.

Solution.

Dans cet exemple . Ainsi,

Regardons le cas de la recherche de la dérivée du produit de trois fonctions. En principe, en utilisant le même système, il est possible de différencier le produit de quatre, cinq et vingt-cinq fonctions.

Exemple.

Effectuer la différenciation de la fonction.

Solution.

Nous partirons de la règle de différenciation du produit de deux fonctions. Comme fonction f(x) on considérera le produit (1+x)sinx, et comme g(x) on prendra lnx :

Pour trouver Nous appliquons à nouveau la règle de la dérivée du produit :

Nous utilisons la règle de la somme dérivée et la table dérivée :

Remplaçons le résultat :

Comme vous pouvez le constater, il faut parfois appliquer plusieurs règles de différenciation dans un même exemple. Il n'y a rien de compliqué là-dedans, l'essentiel est d'agir de manière cohérente et de ne pas tout mélanger.

Exemple.

Trouvez la dérivée de la fonction.

Solution.

La fonction représente la différence des expressions et , donc

Dans la première expression on retire les deux du signe dérivé, et à la seconde expression on applique la règle de différenciation du produit :

Dérivée du quotient de deux fonctions (dérivée d'une fraction).

Montrons la règle pour différencier le quotient de deux fonctions (fractions) . Il convient de mentionner que g(x) ne disparaît pour aucun x dans l’intervalle X.

L’opération consistant à trouver la dérivée est appelée différenciation.

À la suite de la résolution des problèmes de recherche des dérivées des fonctions les plus simples (et pas très simples) en définissant la dérivée comme la limite du rapport de l'incrément à l'incrément de l'argument, un tableau de dérivées et des règles de différenciation précisément définies sont apparus . Les premiers à travailler dans le domaine de la recherche de dérivés furent Isaac Newton (1643-1727) et Gottfried Wilhelm Leibniz (1646-1716).

Par conséquent, à notre époque, pour trouver la dérivée d'une fonction, vous n'avez pas besoin de calculer la limite mentionnée ci-dessus du rapport de l'incrément de la fonction à l'incrément de l'argument, mais il vous suffit d'utiliser le tableau de dérivés et les règles de différenciation. L'algorithme suivant convient pour trouver la dérivée.

Pour trouver la dérivée, il vous faut une expression sous le signe premier décomposer des fonctions simples en composants et déterminer quelles actions (produit, somme, quotient) ces fonctions sont liées. Ensuite, on retrouve les dérivées des fonctions élémentaires dans le tableau des dérivées, et les formules des dérivées du produit, de la somme et du quotient - dans les règles de différenciation. La table des dérivées et les règles de différenciation sont données après les deux premiers exemples.

Exemple 1. Trouver la dérivée d'une fonction

Solution. À partir des règles de différenciation, nous découvrons que la dérivée d'une somme de fonctions est la somme des dérivées de fonctions, c'est-à-dire

À partir du tableau des dérivées, nous découvrons que la dérivée de « X » est égale à un et que la dérivée du sinus est égale au cosinus. Nous substituons ces valeurs dans la somme des dérivées et trouvons la dérivée requise par la condition du problème :

Exemple 2. Trouver la dérivée d'une fonction

Solution. On différencie comme dérivée d'une somme dont le deuxième terme a un facteur constant, il peut être soustrait du signe dérivé :

Si des questions se posent encore quant à l'origine de quelque chose, elles sont généralement éclaircies après familiarisation avec le tableau des dérivées et les règles de différenciation les plus simples. Nous passons à eux en ce moment.

Tableau des dérivées de fonctions simples

1. Dérivée d'une constante (nombre). N'importe quel nombre (1, 2, 5, 200...) présent dans l'expression de fonction. Toujours égal à zéro. Il est très important de s’en souvenir, car cela est très souvent nécessaire.
2. Dérivée de la variable indépendante. Le plus souvent « X ». Toujours égal à un. Il est également important de s'en souvenir longtemps
3. Dérivé du degré. Lorsque vous résolvez des problèmes, vous devez convertir des racines non carrées en puissances.
4. Dérivée d'une variable à la puissance -1
5. Dérivée de racine carrée
6. Dérivée du sinus
7. Dérivée du cosinus
8. Dérivée de la tangente
9. Dérivée de cotangente
10. Dérivée de l'arc sinus
11. Dérivée de l'arccosinus
12. Dérivée de l'arctangente
13. Dérivée de l'arc cotangent
14. Dérivée du logarithme népérien
15. Dérivée d'une fonction logarithmique
16. Dérivée de l'exposant
17. Dérivée d'une fonction exponentielle

Règles de différenciation

1. Dérivée d'une somme ou d'une différence
2. Dérivé du produit
2a. Dérivée d'une expression multipliée par un facteur constant
3. Dérivée du quotient
4. Dérivée d'une fonction complexe

Règle 1.Si les fonctions

sont différentiables à un moment donné, alors les fonctions sont différentiables au même point

et

ceux. la dérivée d'une somme algébrique de fonctions est égale à la somme algébrique des dérivées de ces fonctions.

Conséquence. Si deux fonctions différentiables diffèrent par un terme constant, alors leurs dérivées sont égales, c'est-à-dire

Règle 2.Si les fonctions

sont différentiables à un moment donné, alors leur produit est différentiable au même point

et

ceux. La dérivée du produit de deux fonctions est égale à la somme des produits de chacune de ces fonctions et de la dérivée de l'autre.

Corollaire 1. Le facteur constant peut être soustrait du signe de la dérivée:

Corollaire 2. La dérivée du produit de plusieurs fonctions différentiables est égale à la somme des produits de la dérivée de chaque facteur et de tous les autres.

Par exemple, pour trois multiplicateurs :

Règle 3.Si les fonctions

différenciable à un moment donné Et , alors à ce stade leur quotient est également dérivableu/v, et

ceux. la dérivée du quotient de deux fonctions est égale à une fraction dont le numérateur est la différence entre les produits du dénominateur et la dérivée du numérateur et le numérateur et la dérivée du dénominateur, et le dénominateur est le carré de l'ancien numérateur.

Où chercher des choses sur d'autres pages

Pour trouver la dérivée d'un produit et d'un quotient dans des problèmes réels, il est toujours nécessaire d'appliquer plusieurs règles de différenciation à la fois, il y a donc plus d'exemples sur ces dérivées dans l'article"Dérivée du produit et quotient des fonctions".

Commentaire. Il ne faut pas confondre une constante (c'est-à-dire un nombre) avec un terme dans une somme et comme un facteur constant ! Dans le cas d'un terme, sa dérivée est égale à zéro, et dans le cas d'un facteur constant, elle est soustraite du signe des dérivées. Il s'agit d'une erreur typique qui se produit au stade initial de l'étude des dérivées, mais à mesure que l'étudiant moyen résout plusieurs exemples en une ou deux parties, il ne commet plus cette erreur.

Et si, pour différencier un produit ou un quotient, vous disposez d'un terme toi"v, dans lequel toi- un nombre, par exemple 2 ou 5, c'est-à-dire une constante, alors la dérivée de ce nombre sera égale à zéro et, par conséquent, le terme entier sera égal à zéro (ce cas est abordé dans l'exemple 10).

Une autre erreur courante consiste à résoudre mécaniquement la dérivée d’une fonction complexe comme la dérivée d’une fonction simple. C'est pourquoi dérivée d'une fonction complexe un article séparé est consacré. Mais nous allons d’abord apprendre à trouver les dérivées de fonctions simples.

En chemin, on ne peut pas se passer de transformer les expressions. Pour ce faire, vous devrez peut-être ouvrir le manuel dans une nouvelle fenêtre. Des actions avec des pouvoirs et des racines Et Opérations avec des fractions .

Si vous cherchez des solutions aux dérivées de fractions avec des puissances et des racines, c'est-à-dire lorsque la fonction ressemble à , puis suivez la leçon « Dérivée de sommes de fractions avec puissances et racines ».

Si vous avez une tâche comme , alors vous suivrez la leçon « Dérivées de fonctions trigonométriques simples ».

Exemples étape par étape - comment trouver la dérivée

Exemple 3. Trouver la dérivée d'une fonction

Solution. Nous définissons les parties de l'expression de fonction : l'expression entière représente un produit, et ses facteurs sont des sommes, dans la seconde desquelles l'un des termes contient un facteur constant. On applique la règle de différenciation des produits : la dérivée du produit de deux fonctions est égale à la somme des produits de chacune de ces fonctions par la dérivée de l'autre :

Ensuite, nous appliquons la règle de différenciation des sommes : la dérivée d'une somme algébrique de fonctions est égale à la somme algébrique des dérivées de ces fonctions. Dans notre cas, dans chaque somme le deuxième terme a un signe moins. Dans chaque somme, nous voyons à la fois une variable indépendante dont la dérivée est égale à un et une constante (nombre) dont la dérivée est égale à zéro. Ainsi, « X » devient un et moins 5 devient zéro. Dans la deuxième expression, « x » est multiplié par 2, nous multiplions donc deux par la même unité que la dérivée de « x ». On obtient les valeurs de dérivées suivantes :

Nous substituons les dérivées trouvées dans la somme des produits et obtenons la dérivée de la fonction entière requise par la condition du problème :

Exemple 4. Trouver la dérivée d'une fonction

Solution. Nous devons trouver la dérivée du quotient. On applique la formule de différenciation du quotient : la dérivée du quotient de deux fonctions est égale à une fraction dont le numérateur est la différence entre les produits du dénominateur et la dérivée du numérateur et du numérateur et la dérivée du dénominateur, et le dénominateur est le carré de l’ancien numérateur. On obtient :

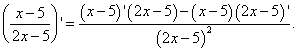
Nous avons déjà trouvé la dérivée des facteurs au numérateur dans l'exemple 2. N'oublions pas non plus que le produit, qui est le deuxième facteur au numérateur dans l'exemple actuel, est pris avec un signe moins :

Si vous cherchez des solutions à des problèmes dans lesquels vous devez trouver la dérivée d'une fonction, où il y a un tas continu de racines et de puissances, comme, par exemple, , alors bienvenue en classe "Dérivée de sommes de fractions avec puissances et racines" .

Si vous avez besoin d'en savoir plus sur les dérivées des sinus, cosinus, tangentes et autres fonctions trigonométriques, c'est-à-dire lorsque la fonction ressemble à , alors une leçon pour toi "Dérivées de fonctions trigonométriques simples" .

Exemple 5. Trouver la dérivée d'une fonction

Solution. Dans cette fonction, nous voyons un produit dont l'un des facteurs est la racine carrée de la variable indépendante, dont nous avons pris connaissance de la dérivée dans le tableau des dérivées. En utilisant la règle de différenciation du produit et la valeur tabulaire de la dérivée de la racine carrée, on obtient :

Exemple 6. Trouver la dérivée d'une fonction

Solution. Dans cette fonction on voit un quotient dont le dividende est la racine carrée de la variable indépendante. En utilisant la règle de différenciation des quotients, que nous avons répétée et appliquée dans l'exemple 4, et la valeur tabulée de la dérivée de la racine carrée, on obtient :

Pour supprimer une fraction du numérateur, multipliez le numérateur et le dénominateur par .