Combinaisons de sudoku. À propos des méthodes de résolution de problèmes - Cours complet de Sudoku

La première chose qui devrait être décidée dans la méthodologie de résolution de problèmes est la question de savoir réellement comprendre ce que nous réalisons et pouvons réaliser en matière de résolution de problèmes. La compréhension est généralement considérée comme allant de soi, et nous perdons de vue le fait que la compréhension a un certain point de départ de la compréhension, seulement par rapport auquel nous pouvons dire que la compréhension a effectivement lieu à partir d'un moment précis que nous avons déterminé. Le Sudoku ici, à notre avis, est pratique dans la mesure où il nous permet de modéliser, dans une certaine mesure, les problèmes de compréhension et de résolution de problèmes. Cependant, nous commencerons par des exemples légèrement différents et non moins importants que le Sudoku.

Un physicien étudiant la relativité restreinte peut parler des propositions « limpides » d’Einstein. Je suis tombé sur cette phrase sur l'un des sites Internet. Mais où commence cette compréhension de la « clarté cristalline » ? Cela commence par l'assimilation de la notation mathématique des postulats, à partir de laquelle toutes les structures mathématiques à plusieurs étages de SRT peuvent être construites selon des règles connues et compréhensibles. Mais ce que le physicien, comme moi, ne comprend pas, c'est pourquoi les postulats de la SRT fonctionnent de telle manière et pas autrement.

Tout d’abord, l’écrasante majorité de ceux qui discutent de cette doctrine ne comprennent pas ce que contient exactement le postulat de la constance de la vitesse de la lumière lorsqu’il est traduit de son application mathématique à la réalité. Et ce postulat implique la constance de la vitesse de la lumière dans tous les sens imaginables et inconcevables. La vitesse de la lumière est constante par rapport à tout objet au repos et en mouvement en même temps. La vitesse d'un faisceau lumineux, selon le postulat, est constante même par rapport au faisceau lumineux venant en sens inverse, transversal et fuyant. Et, en même temps, nous ne disposons en réalité que de mesures indirectement liées à la vitesse de la lumière, interprétée comme sa constance.

Les lois de Newton sont si familières au physicien et même à ceux qui étudient simplement la physique qu'elles semblent si compréhensibles, comme une évidence et il ne peut en être autrement. Mais, disons, l'application de la loi de la gravitation universelle commence par sa notation mathématique, à partir de laquelle même les trajectoires des objets spatiaux et les caractéristiques des orbites peuvent être calculées. Mais nous ne comprenons pas vraiment pourquoi ces lois fonctionnent de cette façon et pas autrement.

Idem avec le Sudoku. Sur Internet, vous pouvez trouver des descriptions répétées de méthodes « de base » pour résoudre les problèmes de Sudoku. Si vous vous souvenez de ces règles, vous pourrez comprendre comment tel ou tel problème de Sudoku est résolu en appliquant les règles « de base ». Mais j’ai une question : comprenons-nous pourquoi ces méthodes « de base » fonctionnent comme elles le font et pas autrement ?

Nous passons donc au prochain point clé de la méthodologie de résolution de problèmes. La compréhension n'est possible que sur la base d'une sorte de modèle qui fournit une base à cette compréhension et la possibilité de réaliser une expérience naturelle ou mentale. Sans cela, on ne peut avoir que des règles d'application de points de départ mémorisés : les postulats du SRT, les lois de Newton ou les méthodes « de base » du Sudoku.

Nous n'avons pas et, en principe, ne pouvons pas avoir de modèles qui satisfassent au postulat de la constance illimitée de la vitesse de la lumière. Nous n'en avons pas, mais des modèles non démontrables et conformes aux lois de Newton peuvent être inventés. Et il existe de tels modèles « newtoniens », mais ils n’impressionnent pas par leurs capacités productives à mener une expérience de pensée ou à grande échelle. Mais le Sudoku nous offre des opportunités que nous pouvons utiliser à la fois pour comprendre les problèmes de Sudoku eux-mêmes et pour illustrer la modélisation en tant qu'approche générale de la résolution de problèmes.

Un modèle possible pour les problèmes de Sudoku est une feuille de travail. Il est créé en remplissant simplement toutes les cellules vides (cellules) du tableau spécifié dans le problème avec les nombres 123456789. Ensuite, la tâche est réduite à supprimer séquentiellement tous les chiffres supplémentaires des cellules jusqu'à ce que toutes les cellules du tableau soient remplies de chiffres uniques (exclusifs) qui satisfont aux conditions du problème.

Je crée une telle feuille de calcul dans Excel. Tout d'abord, je sélectionne toutes les cellules (cellules) vides du tableau. J'appuie sur F5 - "Sélectionner" - "Cellules vides" - "OK". Une manière plus générale de sélectionner les cellules requises : maintenez Ctrl et cliquez sur la souris pour sélectionner ces cellules. Ensuite, pour les cellules sélectionnées, je définis la couleur bleue, la taille 10 (initiale - 12) et la police Arial Narrow. Tout cela pour que les modifications ultérieures du tableau soient clairement visibles. Ensuite, j'entre les nombres 123456789 dans les cellules vides. Je procède comme suit : j'écris et sauvegarde ce numéro dans une cellule séparée. Ensuite, j'appuie sur F2, je sélectionne et copie ce numéro en utilisant Ctrl+C. Ensuite, je vais dans les cellules du tableau et, en parcourant séquentiellement toutes les cellules vides, j'y entre le numéro 123456789 à l'aide de l'opération Ctrl+V, et la feuille de calcul est prête.

Je supprime les numéros supplémentaires, qui seront discutés plus tard, comme suit. À l’aide de l’opération Ctrl+clic, je sélectionne les cellules avec un numéro supplémentaire. Ensuite, j'appuie sur Ctrl+H et saisis le numéro à supprimer dans le champ supérieur de la fenêtre qui s'ouvre, et le champ inférieur doit être complètement vide. Ensuite, cliquez simplement sur l’option « Remplacer tout » et le chiffre supplémentaire sera supprimé.

À en juger par le fait que je peux généralement effectuer un traitement de table plus avancé de la manière « de base » habituelle que dans les exemples donnés sur Internet, la feuille de travail est l'outil le plus simple pour résoudre les problèmes de Sudoku. Par ailleurs, de nombreuses situations concernant l’application des règles dites « de base » les plus complexes ne se sont tout simplement pas présentées dans ma feuille de travail.

En même temps, la feuille de travail est également un modèle sur lequel vous pouvez mener des expériences avec l'identification ultérieure de toutes les règles « de base » et des diverses nuances de leur application découlant des expériences.

Voici donc un fragment d'une feuille de calcul comportant neuf blocs, numérotés de gauche à droite et de haut en bas. Dans ce cas, nous avons le quatrième bloc rempli des numéros 123456789. C'est notre modèle. En dehors du bloc, nous avons surligné en rouge les nombres « activés » (finalement déterminés), en l'occurrence les quatre, que nous comptons insérer dans le tableau en cours d'établissement. Les Blue Five sont des chiffres qui n'ont pas encore été déterminés quant à leur rôle futur, dont nous parlerons plus tard. Les numéros activés que nous avons attribués sont pour ainsi dire barrés, poussés, supprimés - en général, ils déplacent les numéros du même nom dans le bloc, ils y sont donc représentés dans une couleur pâle, symbolisant le fait que ces les nombres pâles sont supprimés. Je voulais rendre cette couleur encore plus pâle, mais elles pourraient alors devenir complètement invisibles lorsqu'elles sont visualisées sur Internet.

En conséquence, dans le quatrième bloc de la cellule E5, il y en avait un, également activé, mais quatre cachés. « Activé » car il peut, à son tour, supprimer les chiffres inutiles s'il y en a qui apparaissent sur son chemin, et « caché » car il se trouve parmi d'autres chiffres. Si la cellule E5 est attaquée par les autres, à l'exception de 4, activés par les numéros 12356789, alors un singleton « nu » apparaîtra dans E5 - 4.

Supprimons maintenant un quatre activé, par exemple de F7. Ensuite, les quatre dans le bloc rempli peuvent se retrouver plus étroits et uniquement dans la cellule E5 ou F5, tout en restant activés dans la ligne 5. Si des cinq activés sont amenés dans cette situation, sans F7=4 et F8=5, alors un activé nu ou caché paire 45.

Après avoir suffisamment travaillé et compris les différentes options avec des simples, des doubles, des triples nus et cachés, etc. non seulement en blocs, mais aussi en lignes et colonnes, nous pouvons passer à une autre expérience. Créons une paire nue 45, comme cela a été fait précédemment, puis connectons les F7=4 et F8=5 activés. En conséquence, la situation E5=45 se présentera. De telles situations surviennent très souvent lors du traitement d’une feuille de calcul. Cette situation signifie que l'un de ces chiffres, dans ce cas 4 ou 5, doit se trouver dans le bloc, la ligne et la colonne qui comprend la cellule E5, car dans tous ces cas, il doit y avoir deux chiffres, pas un seul.

Et surtout, nous savons déjà à quelle fréquence surviennent des situations telles que E5=45. De la même manière, nous définirons des situations où trois chiffres apparaissent dans une cellule, etc. Et quand on ramène le degré de compréhension et de perception de ces situations à un état d’évidence et de simplicité, alors l’étape suivante est, pour ainsi dire, une compréhension scientifique des situations : on pourra alors faire une analyse statistique de tables de Sudoku, identifiez des modèles et utilisez le matériel accumulé pour résoudre les problèmes les plus complexes .

Ainsi, en expérimentant sur le modèle, on obtient une représentation visuelle et même « scientifique » des célibataires, couples, triplés, cachés ou ouverts, etc. Si vous vous limitez uniquement aux opérations avec le modèle simple décrit, certaines de vos idées s'avéreront inexactes, voire erronées. Cependant, dès que l'on passe à la résolution de problèmes précis, les inexactitudes des idées initiales apparaîtront rapidement et les modèles sur lesquels les expériences ont été réalisées devront être repensés et affinés. C'est la voie inévitable des hypothèses et des éclaircissements pour résoudre tout problème.

Il faut dire que les simples cachés et ouverts, ainsi que les paires ouvertes, les triplets et même les quatre, sont des situations courantes qui surviennent lors de la résolution de problèmes de Sudoku avec une feuille de travail. Les couples cachés étaient rares. Mais voici les trois, quatre, etc. cachés. D'une manière ou d'une autre, je n'ai pas rencontré lors du traitement des feuilles de calcul, tout comme les méthodes « X-wing » et « Swordfish » pour contourner les contours, qui ont été décrites à plusieurs reprises sur Internet, dans lesquelles les « candidats » à la suppression apparaissent dans l'une des deux méthodes alternatives. de contourner les contours. Le sens de ces méthodes : si on détruit le « candidat » x1, alors le candidat exclusif x2 reste et en même temps le candidat x3 est supprimé, et si on détruit x2, alors le candidat exclusif x1 reste, mais dans ce cas le candidat x3 est également supprimé, donc dans tous les cas x3 devrait être supprimé, sans affecter les candidats x1 et x2 pour l'instant. Plus généralement, il s'agit d'un cas particulier de la situation : si deux méthodes alternatives conduisent au même résultat, alors ce résultat peut être utilisé pour résoudre un problème de Sudoku. J'ai rencontré des situations dans ce sens plus général, mais pas dans les variantes « x-wing » et « espadon », ni lors de la résolution de problèmes de Sudoku, pour lesquels la connaissance des seules approches « de base » est suffisante.

Les fonctionnalités d'utilisation de la feuille de calcul peuvent être illustrées dans l'exemple non trivial suivant. Sur l'un des forums de solveurs de Sudoku http://zforum.net/index.php?topic=3955.25;wap2, je suis tombé sur un problème présenté comme l'un des problèmes de Sudoku les plus difficiles, qui ne peut être résolu par les méthodes conventionnelles, sans utiliser force brute avec des hypothèses concernant les nombres insérés dans les cellules. Nous allons montrer qu'avec une feuille de calcul vous pouvez résoudre ce problème sans une recherche aussi exhaustive :

A droite se trouve la tâche originale, à gauche se trouve la feuille de travail après « barrée », c'est-à-dire opération de routine consistant à supprimer les chiffres supplémentaires.

Tout d’abord, mettons-nous d’accord sur la notation. ABC4=689 signifie que les cellules A4, B4 et C4 contiennent les nombres 6, 8 et 9 – un ou plusieurs chiffres par cellule. C'est la même chose avec les cordes. Ainsi, B56=24 signifie que les cellules B5 et B6 contiennent les chiffres 2 et 4. Le signe ">" est le signe d'une action conditionnée. Ainsi, D4=5>I4-37 signifie que, en raison du message D4=5, le nombre 37 doit être placé dans la cellule I4. Le message peut être explicite – « nu » – et caché, qui doit être révélé. L'impact d'un message peut être séquentiel (transmis indirectement) le long de la chaîne ou parallèle (impact directement sur d'autres cellules). Par exemple:

D3 = 2 ; D8=1>A9-1>A2-2>A3-4,G9-3; (D8=1)+(G9=3)>G8-7>G7-1>G5-5

Cette entrée signifie que D3=2, mais ce fait doit être révélé. D8=1 transmet son influence à A3 le long de la chaîne et 4 doit être écrit en A3 ; simultanément D3=2 agit directement sur G9, ce qui donne le résultat G9-3. (D8=1)+(G9=3)>G8-7 – l'influence combinée des facteurs (D8=1) et (G9=3) conduit au résultat G8-7. Etc.

Les enregistrements peuvent également contenir des combinaisons telles que H56/68. Cela signifie que les chiffres 6 et 8 sont interdits dans les cellules H5 et H6, soit ils doivent être retirés de ces cellules.

Commençons donc par travailler avec le tableau et appliquons d'abord la condition bien développée et visible ABC4=689. Cela signifie que dans toutes les autres cellules (sauf A4, B4 et C4) du bloc 4 (milieu, gauche) et de la 4ème rangée, les chiffres 6, 8 et 9 doivent être supprimés :

Nous utilisons B56=24 de la même manière. Au total nous avons D4=5 et (après D4=5>I4-37) HI4=37, et aussi (après B56=24>C6-1) C6=1. Appliquons ceci à la feuille de calcul :

Dans I89=68caché>I56/68>H56-68 : soit dans les cellules I8 et I9, il y a une paire cachée de chiffres 5 et 6, qui interdit la présence de ces chiffres dans I56, ce qui conduit au résultat H56-68. On peut considérer ce fragment différemment, tout comme nous l'avons fait dans les expériences sur le modèle de feuille de travail : (G23=68)+(AD7=68)>I89-68 ; (I89=68)+(ABC4=689)>H56-68. C'est-à-dire qu'une « attaque » bidirectionnelle (G23=68) et (AD7=68) conduit au fait que seuls les nombres 6 et 8 peuvent être dans I8 et I9 est ensuite connecté au « . attaque » sur H56 avec les conditions précédentes, ce qui conduit à H56-68. De plus, (ABC4=689) est lié à cette « attaque », ce qui dans cet exemple semble inutile. Cependant, si nous travaillions sans feuille de calcul, alors le facteur d'impact (ABC4=689) serait caché, et il serait assez il convient d'y prêter une attention particulière.

Action suivante : I5=2>G1-2,G6-9,B6-4,B5-2.

J'espère que c'est déjà clair sans commentaires : remplacez les chiffres qui apparaissent après le tiret, vous ne vous tromperez pas :

H7=9>I7-4; D6=8>D1-4,H6-6>H5-8 :

La série d'actions suivante :

D3 = 2 ; D8=1>A9-1>A2-2>A3-4,G9-3;

(D8=1)+(G9=3)>G8-7>G7-1>G5-5;

D5=9>E5-6>F5-4 :

I=4>C9-4>C7-2>E9-2>EF7-35>B7-7,F89-89,

c'est-à-dire qu'en raison du "rayage" - en supprimant les chiffres supplémentaires - une paire ouverte et "nue" 89 apparaît dans les cellules F8 et F9, qui, avec d'autres résultats indiqués dans l'entrée, est appliquée au tableau :

H2=4>H3-1>F2-1>F1-6>A1-3>B8-3,C8-5,H1-7>I2-5>I3-3>I4-7>H4-3

Leur résultat :

Suivez ensuite des actions assez routinières et évidentes :

H1=7>C1-8>E1-5>F3-7>E2-9>E3-8,C3-9>B3-5>B2-6>C2-7>C4-6>A4-9>B4- 8 ;

B2=6>B9-9>A8-6>I8-8>F8-9>F9-8>I9-6 ;

E7=3>F7-5,E6-7>F6-3

Leur résultat : la solution finale au problème :

D'une manière ou d'une autre, nous supposerons que nous avons découvert les méthodes « de base » du Sudoku ou d'autres domaines d'application intellectuelle sur la base d'un modèle approprié et que nous avons même appris à les utiliser. Mais cela ne représente qu’une partie de nos progrès en matière de méthodologie de résolution de problèmes. Vient ensuite, je le répète, l'étape pas toujours prise en compte, mais indispensable, consistant à amener les méthodes précédemment apprises à un état de facilité d'utilisation. Résoudre des exemples, comprendre les résultats et les méthodes de cette solution, repenser ce matériel sur la base du modèle adopté, réfléchir à nouveau à toutes les options, amener le degré de leur compréhension à l'automatisme, lorsque la solution utilisant des dispositions « de base » devient routinière et disparaît comme un problème. Ce que cela donne : tout le monde devrait en faire l’expérience. Mais le fait est que lorsqu'une situation problématique devient routinière, le mécanisme de recherche de l'intellect est orienté vers la maîtrise de dispositions de plus en plus complexes dans le domaine des problèmes à résoudre.

Que sont les « dispositions plus complexes » ? Ce ne sont là que de nouvelles dispositions « fondamentales » pour résoudre le problème, dont la compréhension, à son tour, peut également être amenée à un état de simplicité si un modèle approprié est trouvé à cet effet.

Dans l'article de Vasilenko S.L. "Number Harmony Sudoku" Je trouve un exemple de problème avec 18 touches symétriques :

Concernant ce problème, il est avancé qu'il ne peut être résolu en utilisant des techniques « de base » que jusqu'à un certain état, après quoi il ne reste plus qu'à appliquer une recherche simple avec une substitution d'essai de certains chiffres supposés exclusifs (simples, uniques). dans les cellules. Cet état (un peu plus avancé que dans l’exemple de Vasilenko) a la forme :

Il existe un tel modèle. Il s'agit d'une sorte de mécanisme de rotation pour les numéros exclusifs (uniques) identifiés et non identifiés. Dans le cas le plus simple, un certain trio de chiffres exclusifs tourne dans le sens droit ou gauche, déplaçant ce groupe de ligne en ligne ou de colonne en colonne. En général, trois groupes de triplets de nombres tournent dans un sens. Dans des cas plus complexes, trois paires de chiffres exclusifs tournent dans un sens et un triplet de chiffres simples tourne dans le sens opposé. Ainsi, par exemple, les chiffres exclusifs des trois premières lignes du problème considéré subissent une rotation. Et ce qui est le plus important ici, c'est que ce type de rotation peut être remarqué en examinant la disposition des nombres dans la feuille de calcul traitée. Ces informations sont suffisantes pour l'instant et nous comprendrons d'autres nuances du modèle de rotation en cours de résolution du problème.

Ainsi, dans les trois premières lignes (1, 2 et 3), nous pouvons remarquer la rotation des paires (3+8) et (7+9), ainsi que (2+x1) avec un x1 inconnu et un triple de simples (x2+4+ 1) avec x2 inconnu. Ce faisant, nous pouvons constater que x1 et x2 peuvent chacun être 5 ou 6.

Les lignes 4, 5 et 6 regardent les paires (2+4) et (1+3). Il devrait également y avoir une troisième paire inconnue et un triplet de simples, dont un seul chiffre, 5, est connu.

De même, on regarde les lignes 789, puis les triplets des colonnes ABC, DEF et GHI. Nous noterons les informations collectées sous une forme symbolique et, je l'espère, tout à fait compréhensible :

Pour l’instant, nous n’avons besoin de ces informations que pour comprendre la situation générale. Réfléchissez bien et nous pourrons ensuite passer au tableau suivant spécialement préparé à cet effet :

J'ai mis en évidence des options alternatives avec des couleurs. Le bleu signifie « autorisé » et le jaune signifie « interdit ». Si, disons, A2=79 est autorisé dans A2=7, alors C2=7 est interdit. Ou vice versa – A2=9 est autorisé, C2=9 est interdit. Et puis les autorisations et interdictions sont transmises le long d'une chaîne logique. Cette coloration est conçue pour faciliter la visualisation des différentes options alternatives. En général, il s'agit d'une analogie avec les méthodes « x-wing » et « espadon » mentionnées précédemment lors du traitement des tables.

En regardant l’option B6=7 et, par conséquent, B7=9, nous pouvons immédiatement détecter deux points incompatibles avec cette option. Si B7 = 9, alors dans les lignes 789 apparaît un triple à rotation synchrone, ce qui est inacceptable, puisque soit seulement trois paires (et trois simples de manière asynchrone avec elles) soit trois triples (sans simple) peuvent tourner de manière synchrone (dans une direction). De plus, si B7=9, alors après plusieurs étapes de traitement de la feuille de calcul en 7ème ligne nous trouverons une incompatibilité : B7=D7=9. Nous substituons donc la seule acceptable des deux options alternatives B6 = 9, et le problème est alors résolu en utilisant des moyens simples de traitement conventionnel sans aucune recherche aveugle :

Ensuite, j'ai un exemple prêt à l'emploi utilisant le modèle de rotation pour résoudre un problème du Championnat du Monde de Sudoku, mais j'omet cet exemple afin de ne pas rendre cet article trop long. De plus, il s'est avéré que ce problème a trois solutions possibles, ce qui ne convient pas au développement initial du modèle de rotation des chiffres. J'ai également passé pas mal de temps à étudier le problème de Gary McGuire, extrait d'Internet, avec 17 clés pour résoudre son énigme, jusqu'à ce que, avec une irritation encore plus grande, je découvre que ce « puzzle » a plus de 9 000 solutions possibles.

Bon gré mal gré, nous devons donc passer au problème de Sudoku « le plus difficile au monde », développé par Arto Incala, qui, comme nous le savons, a une solution unique.

Après avoir saisi deux nombres exclusifs très évidents et traité la feuille de calcul, le problème ressemble à ceci :

Les touches affectées à la tâche d'origine sont surlignées en noir et en caractères plus grands. Pour avancer dans la résolution de ce problème, il faut là encore s’appuyer sur un modèle adéquat et adapté à cet effet. Ce modèle est une sorte de mécanisme de rotation des nombres. Il a déjà été discuté plus d'une fois dans cet article et dans des articles précédents, mais afin de comprendre la suite de l'article, ce mécanisme doit être réfléchi et élaboré en détail. C'est à peu près la même chose que si vous aviez travaillé avec un tel mécanisme pendant dix ans. Mais vous pourrez toujours comprendre ce matériel, sinon dès la première lecture, du moins dès la deuxième ou la troisième, etc. De plus, si vous faites preuve de persévérance, alors vous amènerez ce matériel « difficile à comprendre » à l'état de routine et de simplicité. Il n'y a rien de nouveau à cet égard : ce qui est au début très difficile devient progressivement moins difficile, et avec une élaboration continue, tout ce qui est le plus évident et ne nécessite pas d'effort mental tombe à sa place, après quoi vous pouvez libérer votre potentiel mental pour progresser davantage sur le problème donné en cours de résolution ou sur d’autres problèmes.

Après une analyse minutieuse de la structure du problème d'Arto Incal, on peut remarquer que tout est construit sur le principe de trois paires à rotation synchrone et de trois simples tournant de manière asynchrone en paires : (x1+x2)+(x3+x4)+(x5 +x6)+(x7+x8+x9). L'ordre de rotation pourrait par exemple être le suivant : dans les trois premières lignes 123, le premier couple (x1+x2) passe de la première ligne du premier bloc à la deuxième ligne du deuxième bloc, puis à la troisième ligne. du troisième bloc. La deuxième paire se déplace de la deuxième rangée du premier bloc à la troisième rangée du deuxième bloc, puis, dans cette rotation, saute à la première rangée du troisième bloc. La troisième paire de la troisième ligne du premier bloc saute dans la première ligne du deuxième bloc puis, dans le même sens de rotation, passe dans la deuxième ligne du troisième bloc. Le triple des simples se déplace selon un mode de rotation similaire, mais dans le sens opposé à la rotation des paires. La situation avec les colonnes semble similaire : si la table est tournée mentalement (ou réellement) de 90 degrés, alors les lignes deviendront des colonnes, avec le même schéma de mouvement des simples et des paires qu'auparavant pour les lignes.

En effectuant ces rotations dans notre esprit en relation avec le problème d'Arto Incala, on comprend progressivement les restrictions évidentes sur le choix des options de cette rotation pour le triplet de lignes ou de colonnes sélectionné :

Il ne devrait pas y avoir de triolets et de paires tournant de manière synchrone (dans la même direction) - de tels triolets, contrairement au triplet de célibataires, seront appelés triplés à l'avenir ;

Il ne devrait y avoir aucune paire asynchrone ni simple asynchrone ;

Il ne devrait pas y avoir de paires ou de célibataires tournant dans la même direction (par exemple, à droite) - il s'agit d'une répétition des restrictions précédentes, mais cela semblera peut-être plus compréhensible.

De plus, il existe d'autres restrictions :

Il ne doit pas y avoir une seule paire sur 9 lignes qui corresponde à une paire dans l’une des colonnes, et il en va de même pour les colonnes et les lignes. Cela devrait être évident : car le fait même que deux nombres soient situés sur la même ligne indique qu'ils se trouvent dans des colonnes différentes.

On peut aussi dire qu'il y a très rarement des coïncidences de paires dans différents triplets de lignes ou une coïncidence similaire dans des triplets de colonnes, et aussi rarement des coïncidences de triplets de simples dans des lignes et/ou des colonnes, mais celles-ci sont, pour ainsi dire, probabilistes. motifs.

Etude des blocs 4,5,6.

Dans les blocs, 4 à 6 paires (3+7) et (3+9) sont possibles. Si on accepte (3+9), on obtient une rotation synchrone inacceptable du triplet (3+7+9), donc on a une paire (7+3). Après substitution de ce couple et traitement ultérieur du tableau par des moyens classiques, on obtient :

En même temps, on peut dire que 5 dans B6=5 ne peut être qu'un singleton, asynchrone (7+3), et 6 dans I5=6 est paragénératif, puisqu'il est dans la même ligne H5=5 dans le sixième bloc et, par conséquent, elle ne peut pas être seule et ne peut se déplacer que de manière synchrone avec (7+3.

et a classé les candidats pour les célibataires en fonction du nombre de fois où ils sont apparus dans ce rôle dans ce tableau :

Si l'on admet que les 2, 4 et 5 les plus fréquents sont des simples, alors selon les règles de rotation, seules les paires peuvent être combinées avec eux : (7+3), (9+6) et (1+8) - paire (1 +9) rejeté car il annule la paire (9+6). De plus, après avoir substitué ces paires et ces simples et traité davantage le tableau à l'aide de méthodes conventionnelles, nous obtenons :

C’est ainsi que la table s’est révélée indisciplinée : elle ne veut pas être traitée jusqu’au bout.

Il faudra vous forcer et remarquer que dans les colonnes ABC il y a une paire (7+4) et que 6 se déplace de manière synchrone avec 7 dans ces colonnes, donc 6 est un paragénérateur, donc dans la colonne « C » du 4ème bloc uniquement des combinaisons (6+3) sont possibles +8 ou (6+8)+3. La première de ces combinaisons ne fonctionne pas, car dans le 7ème bloc de la colonne «B», un triplet synchrone invalide apparaîtra - un triplet (6+3+8). Eh bien, après avoir remplacé l’option (6+8)+3 et traité le tableau de la manière habituelle, nous arrivons à la réussite de la tâche.

Deuxième option : revenons au tableau obtenu après avoir identifié la combinaison (7+3)+5 dans les lignes 456 et passons à l'examen des colonnes ABC.

Ici, nous pouvons remarquer que la paire (2+9) ne peut pas apparaître dans ABC. D'autres combinaisons (2+4), (2+7), (9+4) et (9+7) donnent un triolet synchrone en A4+A5+A6 et B1+B2+B3, ce qui est inacceptable. Il reste une paire acceptable (7+4). De plus, 6 et 5 déplacent 7 de manière synchrone, ce qui signifie qu'ils sont paragénérés, c'est-à-dire formez des paires, mais pas 5+6.

Faisons une liste des paires possibles et de leurs combinaisons avec des simples :

La combinaison (6+3)+8 ne fonctionne pas, car sinon, un triplet invalide sera formé dans une colonne (6+3+8), ce qui a déjà été discuté et que l'on peut vérifier encore une fois en cochant toutes les options. Parmi les candidats en simple, le numéro 3 marque le plus de points, et la plus probable de toutes les combinaisons proposées est : (6+8)+3, soit (C4=6 + C5=8) + C6=3, ce qui donne :

Ensuite, le candidat le plus probable pour le solo est soit 2, soit 9 (6 points chacun), cependant, dans chacun de ces cas, le candidat 1 (4 points) reste valable. Commençons par (5+29)+1, où 1 est asynchrone avec 5, c'est-à-dire Mettons 1 de B5=1 comme singleton asynchrone dans toutes les colonnes ABC :

Dans le bloc 7, colonne A, les seules options possibles sont (5+9)+3 et (5+2)+3. Mais nous ferions mieux de faire attention au fait que dans les lignes 1 à 3 apparaissent maintenant les paires (4+5) et (8+9). Leur substitution conduit à un résultat rapide, c'est-à-dire pour terminer la tâche après avoir traité la table en utilisant des moyens normaux.

Eh bien, maintenant, après avoir pratiqué les options précédentes, nous pouvons essayer de résoudre le problème d'Arto Incal sans utiliser d'estimations statistiques.

Nous revenons à la position de départ :

Dans les blocs, 4 à 6 paires (3+7) et (3+9) sont possibles. Si nous acceptons (3+9), nous obtenons une rotation synchrone inacceptable du triplet (3+7+9), donc pour la substitution dans le tableau nous n'avons que l'option (7+3) :

5 ici, comme on le voit, est unique, 6 est paraformant. Options valides dans ABC5 : (2+1)+8, (2+1)+9, (8+1)+9, (8+1)+2, (9+1)+8, (9+1) +2. Mais (2+1) est asynchrone (7+3), donc ce qui reste est (8+1)+9, (8+1)+2, (9+1)+8, (9+1)+2. Dans tous les cas, 1 est synchrone (7+3) et donc paragénératif. Remplaçons 1 à ce titre dans le tableau :

Le chiffre 6 est ici un paragénérateur dans le bloc. 4-6, mais la paire remarquable (6+4) n'est pas dans la liste des paires valides. Par conséquent, le quatre dans A4=4 est asynchrone 6 :

Puisque D4+E4=(8+1) et selon l’analyse de rotation forme ce couple, on obtient :

Si cellules C456=(6+3)+8, alors B789=683, soit on obtient un triplet synchrone, il nous reste donc l'option (6+8)+3 et le résultat de sa substitution :

B2=3 est ici un singleton, C1=5 (asynchrone 3) est un paragénérant, A2=8 est également un paragénérant. B3=7 peut être à la fois synchrone et asynchrone. Nous pouvons désormais faire nos preuves dans des techniques plus complexes. Avec un œil exercé (ou du moins en vérifiant sur un ordinateur), on voit que pour tout état B3=7 - synchrone ou asynchrone - on obtient le même résultat A1=1. Par conséquent, nous pouvons substituer cette valeur à A1 et ensuite, en utilisant des moyens simples et plus ordinaires, accomplir notre tâche, ou plutôt celle d’Arto Incala :

D'une manière ou d'une autre, nous avons pu envisager et même illustrer trois approches générales pour résoudre des problèmes : déterminer le point de compréhension du problème (non pas spéculatif ou aveuglément déclaré, mais un moment réel, à partir duquel on peut parler de compréhension du problème), choisir un modèle qui nous permet de réaliser la compréhension à travers une expérience naturelle ou de pensée et - c'est la troisième - d'amener le degré de compréhension et de perception des résultats obtenus à un état d'évidence et de simplicité. Il existe également une quatrième approche, que j'utilise personnellement.

Chaque personne vit des états dans lesquels les tâches et les problèmes intellectuels auxquels elle est confrontée sont résolus plus facilement que ce n'est habituellement le cas. Ces conditions peuvent être entièrement reproduites. Pour ce faire, vous devez maîtriser la technique consistant à désactiver les pensées. D’abord, au moins pendant une fraction de seconde, puis en étirant de plus en plus ce moment d’arrêt. Je ne peux pas en dire plus, ni plutôt recommander quoi que ce soit à cet égard, car la durée d'utilisation de cette méthode est une affaire purement personnelle. Mais j'ai parfois recours à cette méthode pendant longtemps, lorsque je suis confronté à un problème pour lequel je ne vois pas d'options sur la façon de l'aborder et de le résoudre. En conséquence, tôt ou tard, un prototype approprié d'un modèle émerge des réserves de mémoire, ce qui clarifie l'essence de ce qui doit être résolu.

J'ai résolu le problème d'Incal de plusieurs manières, y compris celles décrites dans les articles précédents. Et j'ai toujours, à un degré ou à un autre, utilisé cette quatrième approche avec arrêt et concentration ultérieure des efforts mentaux. J'ai obtenu la solution la plus rapide au problème par une simple recherche - ce qu'on appelle la "méthode poke" - cependant, en utilisant uniquement des options "longues": celles qui pourraient rapidement conduire à un résultat positif ou négatif. D'autres options m'ont pris plus de temps, car la plupart du temps a été consacré au moins au développement approximatif de la technologie permettant d'utiliser ces options.

Une bonne option est également dans l'esprit de la quatrième approche : se mettre à l'écoute pour résoudre des problèmes de Sudoku, en substituant un seul chiffre dans une cellule dans le processus de résolution du problème. Autrement dit, la plupart de la tâche et ses données « défilent » dans l’esprit. C’est ainsi que se déroule la majeure partie du processus intellectuel de résolution de problèmes, et c’est une compétence qui doit être formée pour améliorer vos capacités de résolution de problèmes. Par exemple, je ne suis pas un solveur professionnel de Sudoku. J'ai d'autres tâches. Mais, néanmoins, je souhaite me fixer l'objectif suivant : acquérir la capacité de résoudre des problèmes de Sudoku d'une complexité accrue, sans feuille de travail et sans recourir à la substitution de plus d'un chiffre dans une cellule vide. Dans ce cas, toute méthode de résolution du Sudoku est autorisée, y compris une simple énumération d'options.

Ce n’est pas par hasard que je rappelle ici l’énumération des options. Toute approche pour résoudre les problèmes de Sudoku implique dans son arsenal un ensemble de certaines méthodes, y compris l'un ou l'autre type de recherche. De plus, chacune des méthodes utilisées en particulier dans le Sudoku ou pour résoudre tout autre problème a son propre domaine d'application efficace. Ainsi, pour résoudre des problèmes de Sudoku relativement simples, les plus efficaces sont les méthodes simples « de base », décrites dans de nombreux articles sur ce sujet sur Internet, et la « méthode de rotation » plus complexe s'avère souvent ici inutile, car elle ne fait que compliquer le déroulement d'une solution simple et, en même temps, quoi -il ​​ne fournit pas de nouvelles informations qui apparaissent lors de la solution du problème. Mais dans les cas les plus difficiles, comme celui d’Arto Incal, la « méthode de rotation » peut jouer un rôle clé.

Le Sudoku dans mes articles n'est qu'un exemple illustratif d'approches de résolution de problèmes. Parmi les problèmes que j'ai résolus, il y en a aussi qui sont d'un ordre de grandeur plus difficiles que le Sudoku. Par exemple, des modèles informatiques de chaudières et de turbines situés sur notre site Internet. Cela ne me dérangerait pas non plus d’en parler. Mais pour l'instant, j'ai choisi le Sudoku afin de montrer assez clairement à mes jeunes concitoyens les chemins et étapes possibles de progression vers l'objectif final des problèmes à résoudre.

C'est tout pour aujourd'hui.

• Tutoriel

1. Les bases

La plupart d’entre nous, hackers, savons ce qu’est le Sudoku. Je ne parlerai pas des règles, mais passerai directement aux méthodes.
Pour résoudre un puzzle, aussi complexe ou simple soit-il, les cellules qu'il est évident de remplir sont d'abord recherchées.

1.1 "Le dernier héros"

Regardons le septième carré. Il n'y a que quatre cellules libres, ce qui signifie que quelque chose peut être rempli rapidement.
"8 "sur D3 remplissage de blocs H3 Et J3; exactement pareil" 8 "sur G5 ferme G1 Et G2
En toute conscience, nous mettons " 8 "sur H1

1.2 "Le Dernier Héros" en ligne

Après avoir examiné les carrés pour trouver des solutions évidentes, nous passons aux colonnes et aux lignes.
Considérons " 4 " sur le terrain. Il est clair que ce sera quelque part dans la ligne UN .
Nous avons" 4 "sur G3 qu'est-ce qui bâille A3, Il y a " 4 "sur F7, nettoyage A7. Et un de plus" 4 " dans le deuxième carré interdit sa répétition pour A4 Et A6.
"Le Dernier Héros" pour notre " 4 " Ce A2

1.3 "Pas le choix"

Parfois, plusieurs raisons expliquent un emplacement particulier. " 4 "V J8 serait un excellent exemple.
Bleu les flèches indiquent qu'il s'agit du dernier nombre possible dans le carré. Rouges Et bleu les flèches nous donnent le dernier numéro de la colonne 8 . Légumes verts les flèches donnent le dernier numéro possible dans la ligne J..
Comme vous pouvez le constater, nous n'avons pas d'autre choix que de mettre ceci " 4 "en place.

1.4 « Qui d'autre si ce n'est moi ? »

Il est plus facile de remplir les chiffres en utilisant les méthodes décrites ci-dessus. Cependant, vérifier le nombre comme dernière valeur possible donne également des résultats. La méthode doit être utilisée lorsqu'il semble que tous les chiffres sont là, mais qu'il manque quelque chose.
"5 "V B1 est placé sur la base du fait que tous les nombres proviennent de " 1 "avant" 9 ", sauf " 5 " est en ligne, colonne et carré (marqué en vert).

Dans le jargon, c'est " Solitaire nu". Si vous remplissez le champ avec des valeurs possibles (candidats), alors dans la cellule, un tel numéro sera le seul possible. En développant cette technique, vous pouvez rechercher " Célibataires cachés" - nombres uniques à une ligne, une colonne ou un carré spécifique.

2. "Le kilomètre nu"

2.1 Couples « nus »

"Couple "nu"" - un ensemble de deux candidats situés dans deux cellules appartenant à un même bloc commun : ligne, colonne, carré.
Il est clair que les bonnes solutions au puzzle ne seront que dans ces cellules et uniquement avec ces valeurs, tandis que tous les autres candidats du bloc général pourront être supprimés.


Il y a plusieurs « couples nus » dans cet exemple.
Rouge en ligne UN cellules mises en surbrillance A2 Et A3, tous deux contenant " 1 " Et " 6 "Je ne sais pas encore exactement comment ils se trouvent ici, mais je peux facilement supprimer tous les autres." 1 " Et " 6 " de la ligne UN(marqué en jaune). Aussi A2 Et A3 appartiennent au même carré, donc on supprime " 1 " depuis C1.

2.2 "Trio"

"Trois nus"- une version compliquée des « couples nus ».
Tout groupe de trois cellules dans un bloc contenant En tout trois candidats est "Trio nu". Lorsqu'un tel groupe est trouvé, ces trois candidats peuvent être retirés des autres cellules du bloc.

Combinaisons de candidats pour "trois nus"ça pourrait être comme ça :

// trois nombres dans trois cellules.
// toutes les combinaisons.
// toutes les combinaisons.

Dans cet exemple, tout est assez évident. Dans le cinquième carré de la cellule E4, E5, E6 contenir [ 5,8,9 ], [5,8 ], [5,9 ] respectivement. Il s’avère qu’en général ces trois cellules ont [ 5,8,9 ], et seuls ces chiffres peuvent être là. Cela nous permet de les supprimer des autres candidats de bloc. Cette astuce nous donne une solution" 3 " pour cellule E7.

2.3 "Les Fab Quatre"

"Les quatre nus" un phénomène très rare, surtout sous sa forme complète, et qui donne pourtant des résultats lorsqu'il est détecté. La logique de la solution est la même que dans "trois nus".

Dans l'exemple ci-dessus, dans le premier carré de la cellule A1, B1, B2 Et C1 contiennent généralement [ 1,5,6,8 ], donc ces nombres n’occuperont que ces cellules et aucune autre. Nous supprimons les candidats surlignés en jaune.

3. « Tout ce qui est secret devient clair »

3.1 Paires cachées

Un excellent moyen d'élargir le champ est de rechercher paires cachées. Cette méthode permet de supprimer les candidats inutiles de la cellule et de permettre le développement de stratégies plus intéressantes.

Dans ce puzzle, nous voyons que 6 Et 7 est dans les premier et deuxième carrés. A part ça 6 Et 7 est dans la colonne 7 . En combinant ces conditions, nous pouvons affirmer que dans les cellules A8 Et A9 Il n'y aura que ces valeurs et nous supprimerons tous les autres candidats.


Un exemple plus intéressant et complexe paires cachées. Le couple [ 2,4 ] V D3 Et E3, nettoyage 3 , 5 , 6 , 7 de ces cellules. Surlignées en rouge se trouvent deux paires cachées composées de [ 3,7 ]. D'une part, ils sont uniques pour deux cellules dans 7 colonne, par contre - pour la ligne E. Les candidats surlignés en jaune sont supprimés.

3.1 Triplés cachés

Nous pouvons développer couples cachésà triplés cachés ou même quatre cachés. Trio caché se compose de trois paires de nombres situés dans un bloc. Tel que, et. Cependant, comme c'est le cas avec "trios nus", chacune des trois cellules ne doit pas nécessairement contenir trois nombres. Fonctionnera total trois nombres dans trois cellules. Par exemple , , . Trois cachés sera masqué par d'autres candidats dans les cellules, vous devez donc d'abord vous assurer que troïka applicable à un bloc spécifique.


Dans cet exemple complexe, il y a deux plans à trois cachés. Le premier, marqué en rouge, dans la colonne UN. Cellule A4 contient [ 2,5,6 ], A7 - [2,6 ] et cellule A9 -[2,5 ]. Ces trois cellules sont les seules qui peuvent en contenir 2, 5 ou 6, ce sont donc les seules qui seront là. Par conséquent, nous supprimons les candidats inutiles.

Deuxièmement, dans la colonne 9 . [4,7,8 ] sont propres aux cellules B9, C9 Et F9. En utilisant la même logique, nous supprimons des candidats.

3.1 Quatre cachés

Excellent exemple quatre cachés. [1,4,6,9 ] dans le cinquième carré ne peut être que dans quatre cellules D4, D6, F4, F6. Suivant notre logique, nous supprimons tous les autres candidats (marqués en jaune).

4. « Sans caoutchouc »

Si l’un des nombres apparaît deux ou trois fois dans le même bloc (ligne, colonne, carré), alors nous pouvons supprimer ce nombre du bloc conjugué. Il existe quatre types de jumelage :

1. Paire ou Trois au carré - s'ils sont situés sur une ligne, vous pouvez alors supprimer toutes les autres valeurs similaires de la ligne correspondante.
2. Paire ou Trois dans un carré - s'ils sont situés dans une colonne, vous pouvez alors supprimer toutes les autres valeurs similaires de la colonne correspondante.
3. Paire ou Trois d'affilée - s'ils sont situés dans un carré, vous pouvez alors supprimer toutes les autres valeurs similaires du carré correspondant.
4. Paire ou Trois dans une colonne - s'ils sont situés dans un carré, vous pouvez alors supprimer toutes les autres valeurs similaires du carré correspondant.

4.1 Paires de pointage, triplés

Laissez-moi vous montrer ce puzzle à titre d'exemple. Sur la troisième place" 3 "est seulement dans B7 Et B9. Suite à la déclaration №1 , nous supprimons les candidats de B1, B2, B3. De même, " 2 " du huitième carré supprime une valeur possible de G2.


Un casse-tête spécial. Très difficile à résoudre, mais si vous regardez attentivement, vous remarquerez plusieurs pointant des paires. Il est clair qu’il n’est pas toujours nécessaire de tous les trouver pour avancer dans la solution, mais chacune de ces découvertes facilite notre tâche.

4.2 Réduire l'irréductible

Cette stratégie implique d'analyser et de comparer soigneusement les lignes et les colonnes avec le contenu des carrés (règles №3 , №4 ).
Considérez la ligne UN. "2 "ne sont possibles que dans A4 Et A5. Suivre la règle №3 , retirer " 2 " leur B5, C4, C5.


Continuons à résoudre l'énigme. Nous avons un seul emplacement " 4 " dans un carré de 8 colonne. Selon la règle №4 , nous supprimons les candidats inutiles et obtenons en plus une solution" 2 " Pour C7.

Je voudrais dire que le Sudoku est une tâche vraiment intéressante et passionnante, une énigme, un puzzle, un puzzle, des mots croisés numériques, vous pouvez l'appeler comme vous voulez. Dont la solution apportera non seulement un réel plaisir aux personnes réfléchies, mais permettra également, au cours d'un jeu passionnant, de développer et d'entraîner la pensée logique, la mémoire et la persévérance.

Pour ceux qui connaissent déjà le jeu sous toutes ses manifestations, les règles sont connues et compréhensibles. Et pour ceux qui envisagent tout juste de se lancer, nos informations peuvent être utiles.

Les règles pour jouer au Sudoku ne sont pas compliquées ; elles se trouvent sur les pages des journaux ou peuvent être trouvées assez facilement sur Internet.

Les points principaux sont disposés sur deux lignes : la tâche principale du joueur est de remplir toutes les cellules avec des nombres de 1 à 9. Cela doit être fait de telle manière que dans une ligne, une colonne et un mini-carré 3x3, aucun des nombres sont répétés deux fois.

Aujourd'hui, nous vous proposons plusieurs options de jeux électroniques, dont plus d'un million d'options de puzzle intégrées à chaque joueur.

Pour plus de clarté et une meilleure compréhension du processus de résolution de l'énigme, considérons l'une des options simples, le premier niveau de difficulté de la série Sudoku-4tune, 6**.

Ainsi, un terrain de jeu est donné, composé de 81 cellules, qui constituent à leur tour : 9 lignes, 9 colonnes et 9 mini-carrés mesurant 3x3 cellules. (Fig.1.)

Ne soyez pas dérouté par la mention supplémentaire d'un jeu électronique. Vous pouvez retrouver le jeu sur les pages des journaux ou des magazines, le principe de base reste le même.

La version électronique du jeu offre de belles opportunités de choisir le niveau de difficulté du puzzle, les options du puzzle lui-même et leur nombre, à la demande du joueur, en fonction de sa préparation.

Lorsque vous allumerez le jouet électronique, des numéros clés seront indiqués dans les cellules du terrain de jeu. Qui ne peut être ni transféré ni modifié. Vous pouvez choisir l'option qui convient le mieux à la solution, à votre avis. En raisonnant logiquement, à partir des nombres donnés, il faut remplir progressivement tout le terrain de jeu avec des nombres de 1 à 9.

Un exemple de la disposition initiale des nombres est présenté sur la figure 2. En règle générale, les numéros clés dans la version électronique du jeu sont marqués d'un trait de soulignement ou d'un point dans la cellule. Afin de ne pas les confondre à l'avenir avec les numéros que vous fixerez.

En regardant le terrain de jeu. Il est nécessaire de décider par où commencer la solution. En règle générale, vous devez déterminer la ligne, la colonne ou le mini-carré comportant le nombre minimum de cellules vides. Dans la version que nous avons présentée, nous pouvons sélectionner immédiatement deux lignes, en haut et en bas. Il ne manque qu'un chiffre à ces lignes. Ainsi, une décision simple est prise, après avoir déterminé les nombres manquants -7 pour la première ligne et 4 pour la dernière, nous les saisissons dans les cellules libres de la Fig. 3.

Le résultat obtenu : deux lignes complétées avec des nombres de 1 à 9 sans répétitions.

Prochain coup. La colonne numéro 5 (de gauche à droite) ne comporte que deux cellules libres. Après réflexion, nous déterminons les nombres manquants - 5 et 8.

Pour obtenir un résultat réussi dans le jeu, vous devez comprendre que vous devez naviguer dans trois directions principales : colonne, ligne et mini-carré.

Dans cet exemple, il est difficile de naviguer uniquement par lignes ou colonnes, mais si vous faites attention aux mini-carrés, cela devient clair. Il est impossible d'inscrire le chiffre 8 dans la deuxième cellule (en partant du haut) de la colonne en question, sinon il y aura deux huit dans la deuxième case mine. De même avec le chiffre 5 pour la deuxième cellule (en bas) et le deuxième mini-carré inférieur de la figure 4 (mauvais emplacement).

Bien que la solution semble correcte pour une colonne de neuf chiffres, dans une colonne, sans répétition, elle contredit les règles de base. Dans les mini-carrés, les nombres ne doivent pas non plus être répétés.

Par conséquent, pour trouver la bonne solution, vous devez entrer 5 dans la deuxième cellule (en haut) et 8 dans la deuxième cellule (en bas). Cette décision est tout à fait conforme aux règles. Pour l’option correcte, voir la figure 5.

Une solution ultérieure à une tâche apparemment simple nécessite un examen attentif du terrain de jeu et l'utilisation de la pensée logique. Vous pouvez à nouveau utiliser le principe du nombre minimum de cellules libres et faire attention aux troisième et septième colonnes (de gauche à droite). Il restait trois cellules vides. Après avoir compté les nombres manquants, nous déterminons leurs valeurs - ce sont 2,3 et 9 pour la troisième colonne et 1,3 et 6 pour la septième. Laissons pour l'instant remplir la troisième colonne, car elle n'a pas de clarté certaine, contrairement à la septième. Dans la septième colonne, vous pouvez immédiatement déterminer l'emplacement du chiffre 6 - il s'agit de la deuxième cellule libre à partir du bas. Sur quoi se base cette conclusion ?

En examinant le mini-carré qui comprend la deuxième cellule, il apparaît clairement qu'il contient déjà les nombres 1 et 3. Parmi les combinaisons numériques 1,3 et 6 dont nous avons besoin, il n'y a pas d'autre alternative. Remplir les deux cellules libres restantes de la septième colonne n'est pas non plus difficile. Étant donné que la troisième ligne contient déjà un 1 rempli, 3 est entré dans la troisième cellule à partir du haut de la septième colonne et 1 est entré dans la seule deuxième cellule libre restante. Pour un exemple, voir la figure 6.

Laissons pour l'instant la troisième colonne pour une compréhension plus claire du moment. Cependant, si vous le souhaitez, vous pouvez noter vous-même et saisir dans ces cellules la version attendue des numéros requis pour l'installation, qui pourront être corrigés si la situation devient plus claire. Les jeux électroniques Sudoku-4tune, série 6** vous permettent de saisir plus d'un chiffre dans les cellules pour un rappel.

Après avoir analysé la situation, nous nous tournons vers le neuvième mini-carré (en bas à droite), dans lequel, après notre décision, il restait trois cellules libres.

Après avoir analysé la situation, vous remarquerez (exemple de remplissage d'un mini-carré) qu'il manque les nombres suivants 2,5 et 8 pour le remplir complètement. Après avoir examiné la cellule libre du milieu, vous constaterez que parmi les nombres nécessaires, il n'y a que 5. s'inscrit ici puisque 2 est présent dans la colonne de cellules du haut, et 8 dans une rangée, qui, en plus du mini-carré, inclut cette cellule. En conséquence, dans la cellule du milieu du dernier mini-carré, nous entrons le chiffre 2 (il n'est inclus ni dans la ligne ni dans la colonne), et dans la cellule du haut de ce carré, nous entrons 8. Ainsi, nous avons le coin inférieur droit (9ème) mini-carré complètement rempli d'un carré avec des nombres de 1 à 9, tandis que les nombres ne sont pas répétés en colonnes ou en lignes, Fig.

Au fur et à mesure que les cellules libres se remplissent, leur nombre diminue et nous nous rapprochons progressivement de la résolution de notre énigme. Mais en même temps, résoudre un problème peut être à la fois simplifié et compliqué. Et la première méthode consistant à remplir le nombre minimum de cellules en lignes, colonnes ou mini-carrés cesse d'être efficace. Parce que le nombre de chiffres explicitement définis dans une ligne, une colonne ou un mini-carré particulier diminue. (Exemple : la troisième colonne que nous avons laissée). Dans ce cas, il est nécessaire d'utiliser la méthode de recherche de cellules individuelles, en définissant des nombres qui ne soulèvent aucun doute.

Dans les jeux électroniques Sudoku-4tune, série 6**, il est possible d'utiliser un indice. Quatre fois par jeu, vous pouvez utiliser cette fonction et l'ordinateur lui-même définira le numéro correct dans la cellule que vous avez choisie. Dans les modèles de la série 8**, une telle fonction n'existe pas et l'utilisation de la deuxième méthode devient la plus pertinente.

Regardons la deuxième méthode dans l'exemple que nous utilisons.

Pour plus de clarté, prenons la quatrième colonne. Le nombre vide de cellules qu'il contient est assez grand, six. Après avoir calculé les nombres manquants, nous les déterminons - ce sont 1,4,6,7,8 et 9. Vous pouvez réduire le nombre d'options en prenant comme base le mini-carré moyen, qui comporte un assez grand nombre de spécifiques nombres et seulement deux cellules libres dans une colonne donnée. En les comparant avec les nombres dont nous avons besoin, nous pouvons voir que 1,6 et 4 peuvent être exclus. Ils ne devraient pas être dans ce mini-carré pour éviter les répétitions. Cela laisse 7, 8 et 9. Veuillez noter que dans la rangée (quatrième à partir du haut), qui comprend la cellule dont nous avons besoin, il y a déjà les numéros 7 et 8 parmi les trois restants dont nous avons besoin. Ainsi, la seule option restante pour cette cellule est le numéro 9, Fig. 8. Il n'y a aucun doute sur l'exactitude de cette option de solution et sur le fait que tous les nombres que nous avons considérés et exclus ont été initialement donnés dans la tâche. C'est-à-dire qu'ils ne sont sujets à aucune modification ou transfert, confirmant le caractère unique du numéro que nous avons choisi pour l'installation dans cette cellule particulière.

En utilisant simultanément deux méthodes en fonction de la situation, en analysant et en réfléchissant logiquement, vous remplirez toutes les cellules vides et parviendrez à la bonne solution à n'importe quel puzzle de Sudoku, et à cette énigme en particulier. Essayez de compléter vous-même la solution de notre exemple de la figure 9 et comparez-la avec la réponse finale présentée sur la figure 10.

Peut-être déterminerez-vous vous-même les points clés supplémentaires pour résoudre des énigmes et développerez votre propre système. Ou suivez nos conseils, ils vous seront utiles et vous permettront de rejoindre un grand nombre d'amoureux et de fans de ce jeu. Nous vous souhaitons bonne chance.

- Il s'agit d'une forme de loisir populaire, qui consiste en un puzzle avec des chiffres, également appelé carré magique. Sa solution vous permet de développer une pensée logique, une attention et une approche analytique. Les avantages du Sudoku résident non seulement dans les bienfaits pour le cerveau, mais aussi dans la capacité d'échapper aux problèmes et de se concentrer pleinement sur la tâche.

Règles du sudoku

Ce puzzle prend peu de place, contrairement aux scanwords, aux mots croisés, etc. Le terrain de jeu se compose de 81 carrés, les cellules sont divisées en petits blocs de 3*3. Il peut facilement tenir sur un morceau de papier. La tâche ressemble à des cellules remplies de manière sélective qui doivent être complétées par des valeurs et remplir l'intégralité du tableau. Au Sudoku, les règles du jeu sont très simples et éliminent les solutions multiples. Chaque ligne ou colonne contient des nombres de 1 à 9. De plus, les valeurs ne sont pas répétées dans un petit bloc.

Le niveau de difficulté du Sudoku varie, qui dépend du nombre de cellules remplies de chiffres et des méthodes de résolution. Il y a généralement environ 5 niveaux, où seuls les vrais maîtres peuvent résoudre le plus difficile.

Le jeu de Sudoku a ses propres règles et secrets. Les énigmes les plus simples peuvent être résolues en quelques minutes par déduction, car il y a toujours au moins une cellule pour laquelle un seul chiffre correspond. Les énigmes complexes de Sudoku peuvent prendre des heures à résoudre. Un puzzle correctement construit n’a qu’une seule solution.

Règles pour résoudre le Sudoku

Pour prendre la bonne décision, vous devez considérer quelques règles simples :

• Un nombre ne peut être écrit dans une cellule que s'il ne se trouve pas dans les lignes horizontales et verticales, ainsi que dans le petit carré 3*3.
• Si cela peut être écrit exclusivement dans une seule cellule.

Si les deux points sont pris en compte, vous pouvez être sûr que la cellule est correctement remplie.

Comment résoudre un Sudoku simple ?

Regardons un exemple spécifique de la façon de résoudre le Sudoku. Le terrain de jeu illustré est une version relativement simple du jeu. Les règles du jeu Sudoku pour les plus simples se résument à identifier les dépendances dans les plans horizontaux et verticaux et dans les carrés individuels.

Par exemple, dans la verticale centrale, il n'y a pas assez de nombres 3, 4, 5. Quatre ne peut pas être dans le carré inférieur, car il y est déjà présent. On peut également éliminer le carré central vide, puisque l'on voit 4 sur une ligne horizontale. Nous en concluons qu'il est situé dans la place supérieure. On peut de même mettre 3 et 5 et obtenir le résultat suivant.

En traçant des lignes dans le petit carré supérieur central 3*3, vous pouvez exclure les cellules qui ne peuvent pas contenir le chiffre 3.

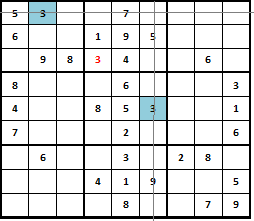
Résoudre En continuant de cette manière, vous devez remplir les cellules restantes. Le résultat est la seule solution correcte.

Certaines personnes appellent cette méthode « Le dernier héros » ou « Loner ». Il est également utilisé comme l'un des nombreux niveaux de maîtrise. Le temps moyen passé sur le niveau de difficulté facile oscille autour de 20 minutes.

Comment résoudre un Sudoku difficile ?

Beaucoup de gens se demandent comment résoudre le Sudoku, s'il existe des méthodes et des stratégies standard. Comme dans tout casse-tête logique. Nous avons examiné le plus simple d'entre eux. Pour passer à un niveau supérieur, il faut avoir plus de temps, de persévérance et de patience. Pour résoudre l'énigme, vous devrez faire des hypothèses et éventuellement obtenir un résultat incorrect, vous ramenant à l'endroit de votre choix. Essentiellement, le Sudoku difficile revient à résoudre un problème à l’aide d’un algorithme. Examinons plusieurs techniques populaires utilisées par les experts professionnels du sudoku en utilisant l'exemple suivant.

Tout d'abord, vous devez remplir les cellules vides avec les options possibles afin de rendre la décision aussi simple que possible et d'avoir une image complète sous vos yeux.

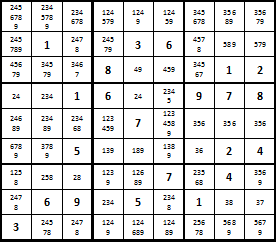
La réponse à la façon de résoudre des puzzles de sudoku complexes est différente pour chacun. Certaines personnes trouvent plus pratique d'utiliser des couleurs différentes pour colorer les cellules ou les nombres, tandis que d'autres préfèrent la version noir et blanc. La figure montre qu'il n'y a pas une seule cellule dans laquelle il y aurait un seul chiffre, cependant, cela ne signifie pas qu'il n'y a pas un seul chiffre dans cette tâche. Armé des règles du Sudoku et d'un examen attentif, vous remarquerez que sur la ligne supérieure du petit bloc du milieu se trouve le chiffre 5, qui n'apparaît qu'une seule fois dans sa ligne. À cet égard, vous pouvez le marquer en toute sécurité et l'exclure des cellules colorées en vert. Cette action entraînera la possibilité de mettre le chiffre 3 dans la cellule orange et de le rayer hardiment des chiffres violets correspondants verticalement et dans le petit bloc 3*3.

De la même manière, nous vérifions les cellules restantes et mettons les unités dans les cellules encerclées, puisqu'elles sont également les seules dans leurs lignes.

Pour savoir comment résoudre des puzzles de Sudoku complexes, vous devez vous armer de plusieurs méthodes simples.

Méthode des paires ouvertes

Pour effacer davantage le champ, vous devez trouver des paires ouvertes qui vous permettent d'exclure les nombres qu'elles contiennent des autres cellules du bloc et des lignes. Dans l'exemple, ces paires sont 4 et 9 de la troisième ligne. Ils montrent clairement comment résoudre des puzzles de Sudoku complexes. Leur combinaison suggère que ces cellules ne peuvent en contenir que 4 ou 9. Cette conclusion est tirée sur la base des règles du Sudoku.

Vous pouvez supprimer les valeurs bleues des cellules surlignées en vert, réduisant ainsi le nombre d'options. Dans ce cas, la combinaison 1249 située dans la première ligne est appelée par analogie « quatre ouverts ». Vous pouvez également trouver des « trois ouverts ». De telles actions entraînent l'apparition d'autres paires ouvertes, comme le 1 et le 2 sur la ligne supérieure, qui permettent également de restreindre l'éventail des combinaisons. En même temps, on met 7 dans la cellule encerclée du premier carré, puisque les cinq de cette ligne seront de toute façon situés dans le bloc inférieur.

Méthode des paires/triples/quatre cachées

Cette méthode est à l’opposé des combinaisons ouvertes. Son essence est que vous devez trouver des cellules dans lesquelles des nombres sont répétés dans un carré/une ligne et que l'on ne trouve pas dans d'autres cellules. Comment cela vous aidera-t-il à résoudre le Sudoku ? Cette technique permet de rayer les nombres restants, car ils servent de fond et ne peuvent pas être placés dans les cellules sélectionnées. Cette stratégie porte plusieurs autres noms, par exemple « La cellule n'est pas en caoutchouc », « Le secret devient apparent ». Les noms eux-mêmes expliquent l'essence de la méthode et le respect de la règle indiquant la possibilité d'inscrire un seul numéro.

Un exemple serait les cellules de couleur bleue. Les chiffres 4 et 7 se trouvent exclusivement dans ces cellules, le reste peut donc être supprimé en toute sécurité.

Le système de conjugaison fonctionne de la même manière, lorsque vous pouvez exclure des cellules d'un bloc/ligne/colonne des valeurs qui apparaissent plusieurs fois dans un bloc adjacent ou conjugué.

Exclusion croisée

Le principe de la résolution du Sudoku réside dans la capacité d'analyse et de comparaison. Une autre façon d'exclure des options est la présence de n'importe quel nombre dans deux colonnes ou lignes qui se croisent. Dans notre exemple, une telle situation ne s’est pas produite, alors considérons-en une autre. L'image montre que le « deux » n'apparaît qu'une seule fois dans les deuxième et troisième blocs du milieu et qu'une fois combinés, ils sont connectés et s'excluent mutuellement. Sur la base de ces données, le chiffre 2 peut être supprimé des autres cellules des colonnes spécifiées.

Peut également être utilisé pour trois et quatre lignes. La complexité de la méthode réside dans les difficultés de visualisation et d'identification des connexions.

Méthode de réduction

À la suite de chaque action, le nombre d'options dans les cellules est réduit et la solution est réduite à la méthode « Unique ». Ce processus peut être appelé réduction et isolé en tant que méthode distincte, car il implique une analyse approfondie de toutes les lignes, colonnes et petits carrés avec l'élimination séquentielle des options. En conséquence, nous arrivons à une solution unique.

Méthode de couleur

Cette stratégie diffère peu de celle décrite et consiste en une indication couleur des cellules ou des nombres. La méthode permet de visualiser l'ensemble du déroulement de la solution, cependant, elle ne convient pas à tout le monde. Pour certains, les couleurs prêtent à confusion et rendent la concentration difficile. Pour utiliser correctement la gamme, vous devez choisir deux ou trois couleurs et peindre les mêmes options dans différents blocs/lignes, ainsi que dans des cellules controversées.

Pour savoir comment résoudre le Sudoku, il est préférable de s'armer d'un stylo et de papier. Cette approche vous permettra d'entraîner votre tête, plutôt que d'utiliser des algorithmes électroniques avec des indices. L'équipe BrainApps a examiné plusieurs des techniques les plus populaires, les plus compréhensibles et les plus efficaces, mais il existe de nombreux autres algorithmes. Par exemple, la méthode « Essai et erreur », lorsqu'une option d'essai est sélectionnée parmi deux ou trois possibles et que toute la chaîne est vérifiée. L'inconvénient de cette technique est la nécessité d'utiliser un ordinateur, car il n'est pas si simple de revenir à la version originale sur une feuille de papier.

Le Sudoku est un puzzle intéressant pour entraîner la logique, contrairement aux puzzles de mots scannés, qui nécessitent de l'érudition et de la mémoire. Le Sudoku a de nombreux pays d'origine, d'une manière ou d'une autre, on le jouait dans la Chine ancienne, au Japon, en Amérique du Nord... Afin que vous et moi apprenions le jeu, nous avons fait une sélection Comment résoudre le Sudoku de facile à difficile.

Pour commencer, disons que le Sudoku est un carré mesurant 9x9, lui-même composé de 9 carrés mesurant 3x3. Chaque carré doit être rempli de chiffres de un à neuf afin que chaque chiffre ne soit utilisé qu'une seule fois le long d'une ligne verticale et horizontale, et uniquement dans un carré de 3x3.

Lorsque vous remplissez toutes les cellules, vous devriez avoir tous les nombres de 1 à 9 dans chacun des 9 carrés. Ainsi, le long de la ligne horizontale, tous les nombres sont de 1 à 9. Et le long de la ligne verticale, la même chose, voir. la photo :

Il semblerait que ce soient des règles simples, mais afin de répondre à la question de savoir comment résoudre le Sudoku, et plus encore, si vous voulez savoir comment résoudre des Sudoku complexes (surtout pour ceux qui commencent tout juste leur parcours), vous devez résoudre au moins quelques problèmes faciles. Il sera alors clair de quoi nous parlons. Ci-dessous les jeux. Essayez de les imprimer et de les remplir pour que tout s'emboîte :

Comment résoudre un Sudoku difficile

J'espère que vous avez lu le texte ci-dessus et résolu la tâche dont vous avez besoin pour comprendre ce qui sera discuté ensuite. Si oui, continuons.

Cette partie de l'article répondra aux questions :

Comment résoudre un Sudoku difficile ?

Comment résoudre le Sudoku : méthodes ?

Comment résoudre le Sudoku : méthodes et méthodes de cellules et de champs ?

Ainsi, on vous a proposé deux jeux, en les résolvant, vous avez acquis des compétences et vous avez eu une idée générale. Afin de vous faire gagner du temps, je vais vous présenter quelques astuces pour résoudre rapidement le Sudoku.

1. Commencez toujours par le numéro 1 et continuez d'abord le long des lignes puis le long des carrés. De cette façon, vous ne vous tromperez certainement pas et vous éviterez de commettre de nombreuses erreurs.

2. Vérifiez toujours quel numéro manque là où il reste moins de cellules vides. Cela permettra de gagner du temps. Et assurez-vous de faire attention au nombre et aux nombres manquants dans le carré 3 x 3 (lignes horizontales et verticales).

3. S'il y a beaucoup de cellules vides dans un carré et que vous arrivez à une impasse, essayez de diviser le carré le long de lignes dans votre esprit. Pensez aux nombres qui peuvent être là, et à partir de là, vous pouvez comprendre quels nombres seront sur les mêmes lignes dans d'autres carrés (et peut-être même comprendre quels nombres seront dans d'autres carrés sur une autre ligne).

4. N’ayez peur de rien, il vaut mieux se tromper et comprendre pourquoi que de ne rien faire !

5. Plus de pratique et vous deviendrez un maître.

Et si les personnes qui résolvent le Sudoku possèdent également une intelligence abstraite, qui donne un puissant potentiel à son propriétaire, alors on peut aller loin. En savoir plus sur ces personnes.

Vous trouverez ci-dessous une sélection de « Comment résoudre un Sudoku difficile », après quoi vous pourrez faire beaucoup de choses !